4.1. Огибающая однопараметрического семейства кривых на плоскости
Определение. Огибающей однопараметрического семейства кривых на плоскости называется кривая, которая в каждой своей точке касается одной из линий семейства.
Пусть однопараметрическое семейство кривых задается уравнением
![]() . (4.1)
. (4.1)
Для вычисления углового коэффициента касательной к линии семейства продифференцируем последнее уравнение по Х в предположении, что У – неявная функция от Х. Предполагаем также, что случай 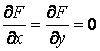 (особые точки семейства) из рассмотрения исключаются.
(особые точки семейства) из рассмотрения исключаются.
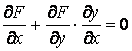 , или
, или 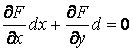 (4.2)
(4.2)
Для записи искомого уравнения огибающей формально используем ту же функцию
![]() ,
,
Где, однако, ![]() – произвольное аналитическое выражение. Отсюда получаем
– произвольное аналитическое выражение. Отсюда получаем
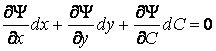 . (4.3)
. (4.3)
Поскольку угловые коэффициенты огибающей и касательной к линиям семейства в точке касания совпадают, то, сравнивая (4.1) и (4.2), получаем, что ![]() . Если
. Если ![]() , то
, то ![]()
![]() , и мы получаем заданное семейство кривых. Поэтому следует считать, что
, и мы получаем заданное семейство кривых. Поэтому следует считать, что ![]() . Окончательно, для определения огибающей получаем систему уравнений
. Окончательно, для определения огибающей получаем систему уравнений
![]() ,
, ![]() . (4.4)
. (4.4)
Исключая из системы параметр С, получим искомое уравнение огибающей.
Заметим, что огибающая семейства кривых может и не существовать, а исключение параметра из системы уравнений (4.4) может привести к геометрическому месту особых точек семейства, в которых кривые не имеют касательных.
Пример. Рассмотрим семейство окружностей заданного радиуса, центры которых лежат на оси ОХ:
![]() .
.
Система уравнений (4.4) принимает вид
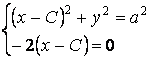 ,
,
Что приводит к двум огибающим семейства ![]() .
.
| < Предыдущая | Следующая > |
|---|