3.9. Асимптотические линии. Геодезическая кривизна. Геодезические линии
Асимптотические линии на поверхности – это линии, в каждой точке которых нормальная кривизна ![]() равна нулю.
равна нулю.
Это возможно, если
1) кривизна ![]() (во всех точках), в этом случае линия – прямая;
(во всех точках), в этом случае линия – прямая;
2) ![]() (
(![]() ),
),
где ![]() – угол между главной нормалью кривой и нормалью к поверхности. Следовательно, главная нормаль лежит в касательной плоскости к поверхности, тогда эта касательная плоскость совпадает с соприкасающейся плоскостью асимптотической линии, а нормаль к поверхности – с ее бинормалью.
– угол между главной нормалью кривой и нормалью к поверхности. Следовательно, главная нормаль лежит в касательной плоскости к поверхности, тогда эта касательная плоскость совпадает с соприкасающейся плоскостью асимптотической линии, а нормаль к поверхности – с ее бинормалью.
Поскольку ![]() , то и
, то и ![]() , тогда
, тогда
![]() . (3.25)
. (3.25)
Условие существования действительных корней для этого уравнения ![]() , а это означает, что асимптотические линии существуют, образуя сеть линий, только в той области поверхности, где ее кривизна отрицательна (все точки гиперболичны). Действительно, из (3.24) следует, что
, а это означает, что асимптотические линии существуют, образуя сеть линий, только в той области поверхности, где ее кривизна отрицательна (все точки гиперболичны). Действительно, из (3.24) следует, что ![]() , так как
, так как ![]() .
.
Пример. Найти асимптотические линии геликоида, уравнения которого рассматривались ранее (раздел 3.4).
Выпишем все необходимые векторы
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() .
.
Вычисляя далее коэффициенты первой и второй квадратичых форм по формулам (3.6) и (3.15), получим
![]() ,
, ![]() ,
, ![]() ,
,
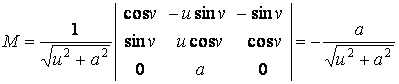 ,
,
Тогда
 ,
,
И уравнение асимптотических линий имеет вид
![]() ,
,
Откуда имеем семейство![]()
![]() – винтовые линии и семейство
– винтовые линии и семейство ![]()
![]() – прямолинейные образующие.
– прямолинейные образующие.
Геодезическая кривизна линии на поверхности определяется формулой
![]() ,
,
Где ![]() – кривизна линии, а
– кривизна линии, а ![]() – угол между главной нормалью линии и нормалью к поверхности. Можно показать, что геодезическая кривизна линии на поверхности зависит только от линейного элемента поверхности и уравнения кривой относительно выбранного ортогонального репера.
– угол между главной нормалью линии и нормалью к поверхности. Можно показать, что геодезическая кривизна линии на поверхности зависит только от линейного элемента поверхности и уравнения кривой относительно выбранного ортогонального репера.
Геодезические линии – это линии с нулевой геодезической кривизной. Из формул для определения геодезической кривизны следует, что геодезическими линиями могут быть либо прямые (![]() ), либо те линии, у которых
), либо те линии, у которых ![]() , т. е.
, т. е. ![]() или
или ![]() . В обоих случаях главная нормаль с точностью до положительного направления совпадает с нормалью к поверхности.
. В обоих случаях главная нормаль с точностью до положительного направления совпадает с нормалью к поверхности.
Сформулируем теорему, которая здесь приводится без доказательства
Теорема. Через всякую точку поверхности в области ее регулярности при заданном угле наклона касательной к направлению первой оси репера проходит одна и только одна геодезическая линия.
Эта теорема аналогична теореме планиметрии: через всякую точку при заданном угле наклона к оси ОХ (заданном направлении) проходит одна и только одна прямая. Однако второе предположение планиметрии – через каждые две точки плоскости проходит одна и только одна прямая – уже не всегда удовлетворяется для геодезических линий на поверхности. В частности, противоположные точки сферы соединяются геодезическими одной длины, образующими однопараметрическое семейство.
Геодезическая линия при заданном линейном элементе поверхности ![]() реализует кратчайшее расстояние между точками А и В По сравнению с другими линиями, проходящими на поверхности через эти точки. Это важное утверждение справедливо при выполнении двух условий:
реализует кратчайшее расстояние между точками А и В По сравнению с другими линиями, проходящими на поверхности через эти точки. Это важное утверждение справедливо при выполнении двух условий:
1) кривые сравнения достаточно близки к данной геодезической;
2) точка В расположена не слишком далеко от точки А.
| < Предыдущая | Следующая > |
|---|