3.8. Полная и средняя кривизна поверхности

Система (3.18) является однородной и линейной относительно неизвестных и . Такая система имеет нетривиальное решение только в том случае, если ее определитель равен нулю

,

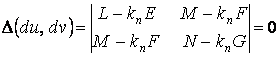Что приводит к квадратному уравнению относительно главных кривизн

. (3.23)

Используя формулы Виета, выпишем сумму и произведение главных кривизн в виде

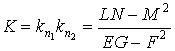, . (3.24)

и называются соответственно средней и полной (гауссовой) кривизнами поверхности. Это основные скалярные инварианты поверхности. Если говорят о поверхностях постоянной кривизны, то имеют в виду полную кривизну поверхности. Обращение в нуль средней кривизны выделяет замечательный класс минимальных поверхностей, которые при заданном контуре имеют наименьшую площадь. Впервые получил эти инварианты Эйлер.

< Предыдущая		Следующая >