3.6. Главные направления и главные кривизны

Среди бесконечного множества значений нормальной кривизны в данной точке поверхности выделим экстремальные. Это так называемые Главные кривизны.

Для определения экстремальных значений нормальной кривизны используем выражение (3.14). Умножая на знаменатель, получаем

, (3.17)

Отношение можно изменять, меняя числитель при постоянном знаменателе, или знаменатель при постоянном числителе. Поэтому мы можем дифференцировать равенство (3.17) по переменной или по переменной . Используем необходимые условия экстремума, приравнивая эти частные производные нулю. Получаем, сокращая на 2

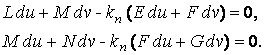(3.18)

Исключая из уравнений (3.18) величину , получаем уравнение

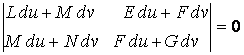, (3.19)

Которое определяет отношение и значение в точке экстремума.

Те направления в точке поверхности, которые дают экстремум нормальной кривизне, называются Главными направлениями.

Теорема. В каждой точке любой поверхности (кроме сферы) существуют в касательной плоскости два действительных, взаимно перпендикулярных главных направления. На сфере главные направления неопределенны.

Здесь необходимо доказать, что квадратное уравнение (3.19) относительно имеет действительные корни. Так как существование главных направлений не зависит от выбора координатных линий, то для упрощения вычислений будем считать координатную систему ортогональной, то есть положим . Тогда уравнение (38) принимает вид

,

Или

, (3.20)

Дискриминант этого квадратного уравнения , так как .

Пусть главным направлениям отвечают решения уравнения (3.20) и . Для доказательства ортогональности рассмотрим выражение

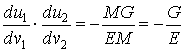
(что следует из квадратного уравнения (3.20)), откуда получим

.

Это совпадает с условиями ортогональности (3.10) при . Если М=0, то уравнение (3.20) принимает вид

, (3.21)

Тогда координатные линии и при ортогональны; если же , то главные направления неопределенные (это верно для сферы).

< Предыдущая		Следующая >