3.5. Вторая квадратичная форма поверхности. Нормальные кривизны. Классификация точек поверхности

Рассмотрим какую–либо линию на поверхности. Пусть в точке М вектор - это единичный вектор нормали к поверхности, а вектора и - единичные вектора касательной и главной нормали к этой линии. Рассмотрим теперь первую формулу Френе . Умножая левую и правую части равенства скалярно на , получаем

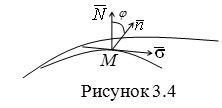
, (3.12)

Где j - угол между векторами и . Так как

,

То

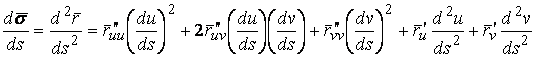.(3.13)

Величину в (3.2) обозначают через и называют Нормальной кривизной поверхности в точке М

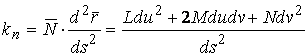, (3.14)

Где (Очевидно, что при вычислении скалярного произведения векторов и (последний вектор определяется равенством (3.13)), имеем , так как вектора и лежат в касательной плоскости к поверхности). Учтем, что единичный вектор нормали

.

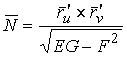Тогда введённые выше коэффициенты можно записать иначе

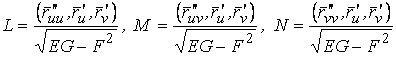, (3.15)

Где числители формул представляют собой смешанные произведения векторов, а коэффициенты E, G и F были определены ранее, формулами (3.6).

Выражение, стоящее в числителе правой части формулы (3.14), называется Второй квадратичной формой поверхности (или Второй дифференциальной формой Гаусса)

, (3.16)

Итак,

И нормальная кривизна равна отношению двух квадратичных форм поверхности.

Как вторая квадратичная форма поверхности, так и нормальная кривизна, не зависят от выбора декартовой системы координат, или от выбора криволинейных координат на поверхности. Поскольку числитель и знаменатель выражения (3.14) –это квадратичные формы относительно , то нормальная кривизна зависит только от отношения , то есть, нормальная кривизна определяется касательной к выбранной кривой на поверхности. Отсюда следует теорема.

Теорема. Все линии на поверхности, проходящие через точку М поверхности с общей касательной имеют одну и ту же нормальную кривизну.

Отметим также, что в так называемых Нормальных сечениях поверхности, проходящих через вектор нормали , направление этого вектора совпадает с направлением главной нормали к линии на поверхности, лежащей в этом сечении, так что нормальная кривизна совпадает с кривизной этой линии. Обычно радиус кривизны нормального сечения поверхности берется с противоположным знаком.

Поскольку , то знак нормальной кривизны 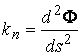полностью определяется знаком числителя, то есть знаком второй квадратичной формы. Разделив выражение на (при , в противном случае нужно делить на ) и обозначая , исследуем знак получившегося квадратичного трехчлена . Если , то, разделив на L, исследуем выражение

.

1) Если , то тогда полученное квадратичное выражение, а значит и положительны. В этом случае в рассматриваемой точке знак нормальной кривизны один и тот же во всех направлениях и определяется только знаком L, а главные нормали всех кривых на поверхности, проходящих через эту точку, направлены в одну сторону. Такая точка называется Эллиптической.

2) Если , то, в зависимости от отношения , вторая квадратичная форма может оказаться как положительной, так и отрицательной, и нормальная кривизна также может менять знак. Такая точка поверхности называется Гиперболической.

3) Если , то и не меняют знака, но обращаются в нуль, если . Эта точка поверхности называется Параболической.

< Предыдущая		Следующая >