3.4. Дифференциал площади поверхности
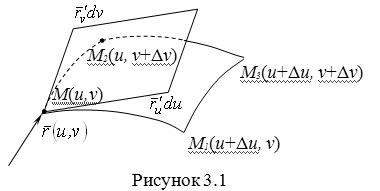
Рассмотрим координатную сеть линий на поверхности и криволинейный четырёхугольник, образованный линиями с постоянными значениями координат U И U+DU, V И V+DV, пересекающимися в точках ![]() (рис. 3.1). Выделяя главные части приращений
(рис. 3.1). Выделяя главные части приращений
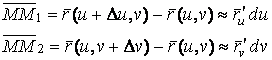
И приближенно (при малых ![]() ) заменяя криволинейный четырёхугольник параллелограммом, построенным на векторах
) заменяя криволинейный четырёхугольник параллелограммом, построенным на векторах ![]() и
и ![]() , как показано на рис. 2.1, запишем площадь параллелограмма в виде
, как показано на рис. 2.1, запишем площадь параллелограмма в виде
![]() .
.
С учётом формулы (3.7) находим
![]() . (3.11)
. (3.11)
Поскольку криволинейный четырёхугольник мало отличается от параллелограмма при ![]() , величину
, величину ![]() называют Дифференциалом площади поверхности
называют Дифференциалом площади поверхности
Пример 1. Геликоид. Эта поверхность получается при винтовом движении отрезка прямой, параллельного плоскости ![]() и пересекающего ось
и пересекающего ось ![]() (ось винтового движения). Проекция отрезка прямой на плоскость
(ось винтового движения). Проекция отрезка прямой на плоскость ![]() равномерно вращается около начала координат, а точка пересечения с осью
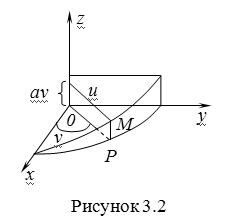
равномерно вращается около начала координат, а точка пересечения с осью ![]() равномерно перемещается по этой оси (рис. 3.2).
равномерно перемещается по этой оси (рис. 3.2).
Запишем вектора
![]() ,
,
![]() ,
,
![]() ,
,

Тогда ![]() ,
, ![]() ,
, ![]() , линейный элемент
, линейный элемент
![]() .
.
Координатные линии здесь записываются таким образом:
– линия ![]()
![]() – винтовая линия; при полном обороте (на угол 2P) проекции
– винтовая линия; при полном обороте (на угол 2P) проекции ![]() точка М поднимается на 2PА, где А – шаг винта;
точка М поднимается на 2PА, где А – шаг винта;
– линия ![]()
![]() во всех точках имеет одну и ту же аппликату
во всех точках имеет одну и ту же аппликату ![]() ; проекция линии на плоскость
; проекция линии на плоскость ![]() Определяется уравнением
Определяется уравнением ![]() .
.
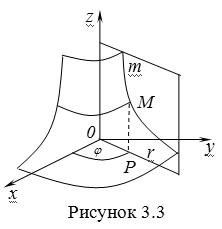 Пример 2. Поверхность вращения. Пусть в плоскости, проходящей через ось Oz , задана линия M
Пример 2. Поверхность вращения. Пусть в плоскости, проходящей через ось Oz , задана линия M
![]() ,
,
Где Z И R - прямоугольные декартовы координаты в этой плоскости, причем ось Or лежит на пересечении этой плоскости с плоскостью XOY. Пусть теперь M вращается вокруг оси Oz. Вводя на плоскости XOY полярные координаты R,J , получаем для точки P (проекции точки M, лежащей на линии M) следующие координаты, которые при вращении линии будут изменяться вместе с углом вращения j
![]() .
.
Точка М имеет эти две координаты и ещё третью координату
![]() .
.
Таким образом, радиус-вектор произвольной точки, лежащей на поверхности вращения, имеет вид
![]() ,
,
![]() ,
, ![]() ,
,
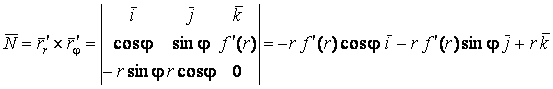 .
.
Тогда
![]() ,
, ![]() ,
, ![]() ,
,
Линейный элемент
![]() .
.
Так как ![]() , то координатные линии образуют ортогональную сеть. Линии j=Const Называются меридианами (они получаются в сечении поверхности плоскостями, проходящими через ось вращения). Линии R=const называются параллелями (они получаются в сечении поверхности плоскостями, перпендикулярными оси Oz), это окружности с центрами на оси Oz.
, то координатные линии образуют ортогональную сеть. Линии j=Const Называются меридианами (они получаются в сечении поверхности плоскостями, проходящими через ось вращения). Линии R=const называются параллелями (они получаются в сечении поверхности плоскостями, перпендикулярными оси Oz), это окружности с центрами на оси Oz.
| < Предыдущая | Следующая > |
|---|