3.2. Первая квадратичная форма поверхности. Дифференциальный элемент площади поверхности

Рассмотрим квадрат дифференциала длины дуги любой линии на поверхности

.

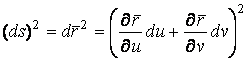Подставляя в это последнее равенство выражения 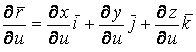и и выделяя коэффициенты при , получаем

, (3.5)

Где

, ,

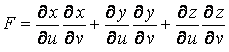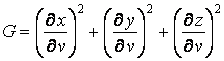. (3.6)

Как видно из последних формул, коэффициенты не зависят от выбора линии на поверхности, а зависят только от вида поверхности и от координат точки.

Квадратичная форма , определённая в (3.5), называется Первой квадратичной формой поверхности (или Первой дифференциальной формой Гаусса, а также Линейным элементом поверхности). Это основная метрическая форма поверхности. Она инвариантна в том смысле, что не меняется при перемещении поверхности как твёрдого тела, и не зависит от преобразования декартовой системы координат.

Если обозначить

, ,

То из (3.6) следует, что

, , ,

Где G – угол между векторами и , то есть угол, под которым пересекаются координатные линии. Кроме того,

. (3.7)

Следовательно, коэффициенты и дискриминант – положительны, а квадратичная форма положительно определена. Коэффициент может быть и положительным, и отрицательным в зависимости от знака , то есть в зависимости от того, будет ли координатный угол острым или тупым. Если , то координатные линии ортогональны и .

Заметим также, что

. (3.8)

< Предыдущая		Следующая >