3.1. Поверхность в пространстве. Касательная плоскость и нормаль к поверхности в пространстве

Известно, что поверхность в пространстве определяется уравнением

, (3.1)

Связывающем прямоугольные декартовые координаты . Другой способ аналитического описания поверхности – использование парaметрических уравнений

. (3.2)

Исключая параметры , мы возвращаемся к уравнению (3.1), связывающему переменные .

Пусть задана некоторая точка на поверхности. Возьмём произвольную кривую, лежащую на поверхности и проходящую через эту точку. Пусть кривая определяется уравнениями

Подставляя эти соотношения в (3.1) и дифференцируя по параметру , получаем

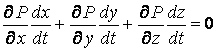. (3.3)

Равенство (3.3) можно рассматривать как условие ортогональности вектора , направленного по касательной к кривой, а значит, и к поверхности, и вектора .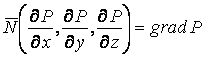

Поскольку кривая выбрана произвольно, то вектор ортогонален ко всем касательным к поверхности, проходящим через точку (эти касательные заполняют касательную плоскость). Вектор называется нормальным вектором плоскости. Уравнения касательной плоскости и нормали к поверхности в точке имеют вид

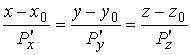, (3.4)

Где все производные вычисляются в точке .

Заметим, что всё здесь сказанное о касательной плоскости и нормали относится к неособым точкам поверхности. Особые точки поверхности, для которых выписанные формулы не имеют смысла, определяются равенствами

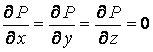Теперь обратимся к параметрическим уравнениям поверхности. Подставляя соотношения (3.2) в уравнения (3.1) и дифференцируя по , имеем

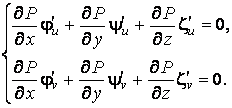
Отсюда получаем, что

, , ,

Где К – некоторая постоянная. Последние равенства дают возможность записать уравнения касательной плоскости и нормали к поверхности, представленные формулами (3.4), в параметрическом виде.

Параметры определяют положение точки на поверхности, поэтому их называют криволинейными координатами на поверхности. Координатные линии или в общем случае будут кривыми линиями. Линия, вдоль которой изменяется только параметр , называется линией , а линия, вдоль которой изменяется только параметр – линией .

< Предыдущая		Следующая >