1.5. Кривизна пространственной кривой и её вычисление

Определение кривизны по формуле (1.5) имеет место и в пространственном случае. В качестве основного “естественного параметра” принимаем длину дуги кривой , так что текущий радиус-вектор кривой запишем как

.

Рассмотрим модуль вектора , а именно

,

Т. е. 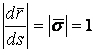в любой точке кривой.

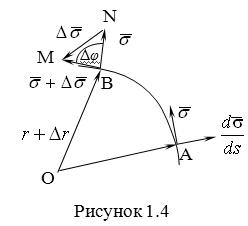
Пусть вектор направлен по касательной к кривой в некоторой точке А (рис.1.4). Задавая приращение параметра , переходим к точке В, а вектор , направленный по касательной к кривой в точке В, обозначим через . Так как , о является равнобедренным, поэтому, обозначив угол поворота касательной через , запишем

.

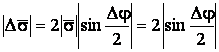Отсюда получаем

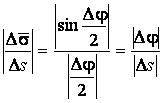
И, следовательно, в пределе при находим, что

,

Как следует из определения кривизны. С другой стороны,

.

Итак, мы получаем следующую формулу для вычисления кривизны

(1.8)

Далее, поскольку – единичный вектор, то из формулы (1.4) следует, что вектор ортогонален вектору и, следовательно, этот последний вектор лежит в нормальной плоскости к кривой в данной её точке. Соответствующее направление называют направлением главной нормали. Обозначив единичный вектор главной нормали через , запишем так называемую Первую формулу Френе

, (1.9)

Где коэффициент пропорциональности и является кривизной, поскольку , т. е. 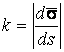. (Направление главной нормали выбирается таким образом, чтобы величина была положительной).

Перейдем теперь к вычислению кривизны в более общем случае, когда радиус-вектор кривой есть функция произвольного параметра . Справедливо равенство

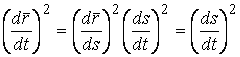, (1.10)

Поскольку ранее было установлено, что .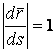

Дифференцируя равенство (1.10) по параметру T, имеем

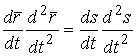. (1.11)

Вновь возводя в квадрат, получим

(1.12)

Теперь вычисляем

И

.

Отсюда

.

В последнюю формулу, исключая естественный параметр , подставим вместо , и соответствующие выражения из вспомогательных формул (1.10), (1.11), (1.12). Получаем

, (1.13)

Где знак ‘‘´’’ означает векторное произведение. В том, что и совпадают, можно легко убедиться непосредственным вычислением (здесь для краткости введён символ (¢) как знак дифференцирования по параметру T). В случае если , из (1.13) получаем

. (1.14)

Если рассматриваемая кривая представляет собой траекторию движения некоторой материальной точки, а – время, то, вводя векторы скорости и ускорения , можно переписать формулу (1.13) в виде

Пример. Винтовая линия, которая задана уравнениями , , , где – некоторые постоянные. Выпишем векторы

и .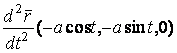

Тогда

;

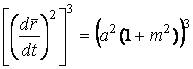И, следовательно,

.

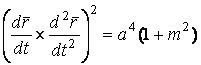Итак, по формуле (1.13)

,

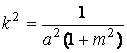Т. е. кривизна винтовой линии одна и та же во всех точках данной кривой.

< Предыдущая		Следующая >