2.1. Формулы Френе. Трёхгранник Френе
В предыдущих параграфах были введены два единичных ортогональных вектора: вектор ![]() , направленный по касательной к кривой, и вектор главной нормали
, направленный по касательной к кривой, и вектор главной нормали ![]() , который определён первой формулой Френе (1.9). Введём единичный вектор
, который определён первой формулой Френе (1.9). Введём единичный вектор ![]() , ортогональный векторам
, ортогональный векторам ![]() и
и ![]() , как векторное произведение
, как векторное произведение ![]() на
на ![]()
![]() . (2.1)
. (2.1)
Нормаль, которая определяется вектором ![]() , называется Бинормалью. Очевидно, что получена правая тройка ортогональных векторов. Этот подвижный базис (или репер), который сопровождает точку М при её движении по кривой, называется Подвижным, а также Естественным базисом или Репером Френе (Френе – французский геометр XIX века, который в 1847 году первым написал формулы для производных по длине дуги трёх базисных векторов
, называется Бинормалью. Очевидно, что получена правая тройка ортогональных векторов. Этот подвижный базис (или репер), который сопровождает точку М при её движении по кривой, называется Подвижным, а также Естественным базисом или Репером Френе (Френе – французский геометр XIX века, который в 1847 году первым написал формулы для производных по длине дуги трёх базисных векторов ![]() ,
, ![]() ,
, ![]() ).
).
Плоскость, проходящая через вектора ![]() и
и ![]() , называется Соприкасающейся, через вектора
, называется Соприкасающейся, через вектора ![]() и
и ![]() – Нормальной, а через вектора
– Нормальной, а через вектора ![]() и
и ![]() – Спрямляющей. Эти три плоскости образуют так называемый Естественный трехгранник, или Трехгранник Френе (рис. 2.1).
– Спрямляющей. Эти три плоскости образуют так называемый Естественный трехгранник, или Трехгранник Френе (рис. 2.1).

Уравнение (1.9) определяет производную ![]() . Для того, чтобы получить производные от векторов
. Для того, чтобы получить производные от векторов ![]() и
и ![]() , обратимся к формуле (2.1). Дифференцируя по
, обратимся к формуле (2.1). Дифференцируя по ![]() и используя формулу (1.9), имеем
и используя формулу (1.9), имеем
![]() .
.
Отсюда следует, что вектора ![]() и
и ![]() ортогональны. Кроме того,
ортогональны. Кроме того, ![]() ортогонально
ортогонально ![]() (см п.3о в 1.2). Таким образом, направление вектора
(см п.3о в 1.2). Таким образом, направление вектора ![]() совпадает с направлением вектора главной нормали
совпадает с направлением вектора главной нормали ![]()
![]() . (2.2)
. (2.2)
Это Вторая формула Френе, где коэффициент ![]() характеризует степень изменяемости вектора
характеризует степень изменяемости вектора ![]() по длине дуги, то есть поворот соприкасающейся плоскости. Если
по длине дуги, то есть поворот соприкасающейся плоскости. Если ![]() , то кривая лежит в этой плоскости. Коэффициент
, то кривая лежит в этой плоскости. Коэффициент ![]() называется кручением.
называется кручением.
Теперь рассмотрим ![]() . Этот вектор ортогонален
. Этот вектор ортогонален ![]() (по формуле (1.4)), поэтому в разложении по ортогональному базису
(по формуле (1.4)), поэтому в разложении по ортогональному базису ![]() ,
, ![]() ,
, ![]() ,
,
![]() , (2.3)
, (2.3)
Коэффициент ![]() .
.
Продифференцируем равенство
![]() :
: ![]() .
.
В последнее соотношение подставим выражение ![]() из (2.3) и
из (2.3) и ![]() из (1.9). Получаем равенство
из (1.9). Получаем равенство ![]() , отсюда коэффициент
, отсюда коэффициент ![]() .
.
Поскольку ![]() , получаем
, получаем
![]() . (2.4)
. (2.4)
С другой стороны, по второй формуле Френе
![]() .
.
Таким образом, С= ![]() , и
, и
![]() . (2.5)
. (2.5)
Это Третья формула Френе.
По определению кривизна ![]() , но кручение
, но кручение ![]() может быть любого знака.
может быть любого знака.
Для вычисления кручения используем вторую формулу Френе ![]() . Умножив скалярно на
. Умножив скалярно на ![]() левую и правую части равенства, получим
левую и правую части равенства, получим
![]() .
.
С учётом равенства ![]() (см. формулу (2.4)), имеем
(см. формулу (2.4)), имеем
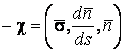 ,
,
Где в круглых скобках записано смешанное произведение трёх векторов. Поскольку ![]() , а из первой формулы Френе следует, что
, а из первой формулы Френе следует, что 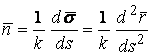 , то
, то
 , (2.6)
, (2.6)
Где в данном случае штрих означает дифференцирование по ![]() .
.
| < Предыдущая | Следующая > |
|---|