1.4. Кривизна плоской кривой и её вычисление

Степень искривленности кривой определяется углом поворота касательной к кривой (углом смежности). Однако этот угол зависит от длины дуги кривой AB (рис.1.2). Введем среднюю кривизну кривой для заданной дуги AB

.

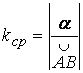Обозначив

,

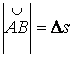запишем .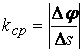

Так как – конечная величина, значение средней кривизны зависит от выбора . Для характеристики степени искривленности (кривизны) кривой в точке необходимо перейти к пределу при .

Определение. Кривизна кривой в точке А равна

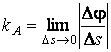. (1.5)

Для получения формулы вычисления кривизны кривой, заданной уравнением в прямоугольных декартовых координатах, используем рис. 1.3.

Исходя из формулы (1.5), запишем

.

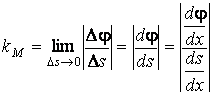Вспоминая геометрический смысл производной, , получаем

,

Тогда 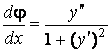(здесь и далее и т. д.), кроме того, . Окончательно

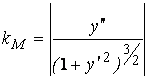. (1.6)

Пример 1. Парабола . Тогда .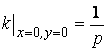

Пример 2. Прямая , здесь и в любой точке.

Пример 3. Окружность радиуса R. Здесь удобнее использовать не формулу (1.5), а выражение для средней кривизны.

.

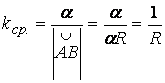Переход к пределу не изменит этого значения, и, следовательно, кривизна в любой точке окружности равна .

Во многих задачах и теоретических выкладках помимо кривизны вводят Радиус кривизны

. (1.7)

< Предыдущая		Следующая >