1.3. Касательная к линии

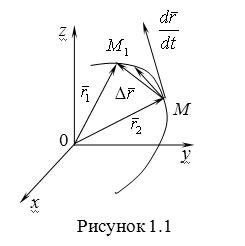Рассмотрим векторное уравнение кривой (1.2). Выделим две точки на кривой М и (рис.1.1), которые соответствуют значениям параметра T и . Хорда, соединяющая точки М и , определяет вектор . При переходе к пределу, когда , точка , двигаясь по дуге , в пределе совпадает с точкой М. При этом при , но отношение может сохранить в пределе конечное значение. Секущая в пределе займет положение касательной к линии в точке М. На этой касательной и будет лежать вектор производной

.

Последний результат можно сформулировать в виде теоремы.

Теорема. Производная от радиус-вектора текущей точки кривой имеет направление касательной к кривой.

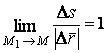Поскольку предел отношения длины дуги к длине хорды равен 1, т. е. , то

.

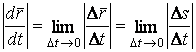< Предыдущая		Следующая >