1.2. Правила дифференцирования вектор-функции скалярного аргумента

1. .

Действительно, приращение суммы функций складывается из приращений слагаемых , отсюда

.

2. ,

Где – дифференцируемая скалярная функция. Действительно,

,

Откуда

,

И после перехода к пределу при получаем то, что и требовалось доказать.

3. ,

Где всюду рассматриваются скалярные произведения векторов. Действительно,

,

Откуда получаем искомое, разделив на и переходя к пределу при .

3°. Следствие. Пусть , где – единичный вектор. Тогда , и из формулы дифференцирования скалярного произведения имеем

(1.4)

Формула (1.4) означает, что Производная единичного вектора ортогональна этому вектору. Этот результат и будет часто использоваться в дальнейшем.

4. ,

Где знак “” является символом векторного произведения. Действительно,

.

Разделив на и переходя к пределу при , получаем выписанную ранее формулу.

5. Для смешанного произведения имеем

.

Доказательство опускаем. Его можно получить без большого труда, комбинируя некоторые предыдущие формулы.

6. Дифференцирование сложной функции. Пусть , , тогда

.

Действительно,

.

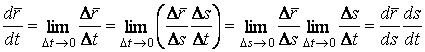7. Для вектор-функции не имеет место теорема Ролля, а значит и теорема Лагранжа. Однако ряд Тейлора с остаточным членом может быть выписан и для вектор-функции.

< Предыдущая		Следующая >