3.7. Каноническое и параметрические уравнения прямой

Составим уравнение прямой, проходящей через данную точку параллельно данному вектору (рис. 22).

Пусть — некоторая прямая на плоскости; заданы точка и вектор = — так называемый Направляющий вектор прямой. Пусть — произвольная текущая точка на прямой . Так как , вектор коллинеарен вектору = . Но у коллинеарных векторов координаты пропорциональны. Записывая данную пропорцию, получаем

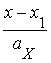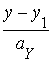= . (11)

Это уравнение называется Каноническим уравнением прямой на плоскости.

Здесь

— координаты точки, через которую проходит прямая,

— координаты направляющего вектора прямой,

— координаты текущих точек прямой.

Пример 27. Составить каноническое уравнение прямой, проходящей через точку и имеющей направляющий вектор = .

Решение.

= ó = ó

Ответ: Искомое уравнение имеет вид . Прямая проходит параллельно оси , пересекая ось в точке .

Рассмотрим снова каноническое уравнение прямой . Обозначив через общее значение данной пропорции, получим:

= = ,

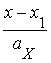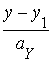Введя обозначения и , получим:

(так называемые Параметрические уравнения прямой на плоскости).

Здесь:

— координаты некоторой точки, через которую проходит прямая;

— координаты текущей точки прямой;

— параметр, через который линейно выражаются координаты точек прямой; — коэффициенты, определяющие координаты направляющего вектора прямой.

Согласно данным уравнениям, каждому значению параметра соответствует определенная точка прямой с координатами .

< Предыдущая		Следующая >