3.6. Уравнение прямой, проходящей через две данные точки
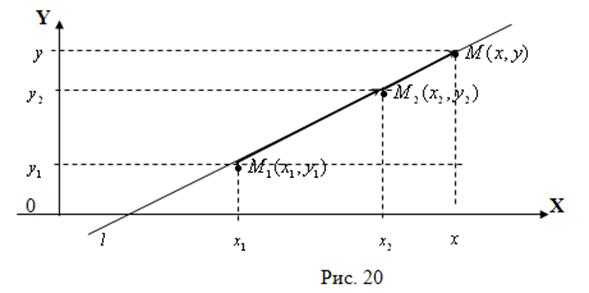
Пусть заданы две точки 
и 
на плоскости. Требуется составить уравнение прямой, проходящей через эти точки (рис. 20).
В силу утверждения 7, у коллинеарных векторов 
и 
координаты должны быть пропорциональны. Отсюда: Уравнение прямой на плоскости, проходящей через точки и , записывается в виде
= 
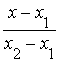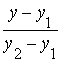, (10)
Где переменные 
— координаты текущих точек прямой. Угловой коэффициент этой прямой находится по формуле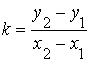 
.
Пример 24. Составить уравнение прямой, проходящей через две точки 
и 
.
= 
ó 
= 
ó 
=
ó 
Ответ: — общее уравнение прямой; 
=
— ее уравнение с угловым коэффициентом.
Пример 25. Составить уравнение прямой, проходящей через две точки и 
.
= 
ó 
= 
ó 
Ответ: Искомое уравнение имеет вид . Прямая проходит параллельно оси 
, пересекая ось 
в точке .
Пример 26. Даны вершины треугольника 
, 
, 
. Найти точку пересечения высоты 
, опущенной из вершины 
, и медианы 
, проведенной из вершины 
, а также острый угол, заключенный между ними (см. рис. 21).
Решение. Используя уравнение (10) прямой, проходящей через две заданные точки, найдем сначала уравнение стороны 
треугольника 
. Получим:
или 
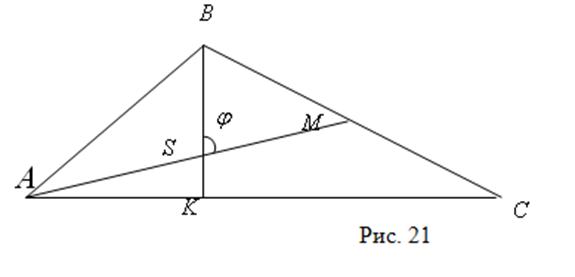
Угловой коэффициент этой прямой равен 
. Так как высота 
, ее угловой коэффициент можно найти по формуле 
. Поскольку нам известна точка , то уравнение высоты находим так: 
. Получаем: 
или 
.
Найдем теперь уравнение медианы . Координаты точки 
(середины отрезка 
) находим по формулам:
.
Имеем: 
.
Используя (10), получим уравнение медианы :
или 
Координаты точки 
пересечения высоты и медианы находим теперь как решение системы уравнений
Имеем: 
.
Наконец, используя формулу (9), находим острый угол 
между и 
:
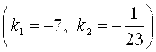| < Предыдущая | Следующая > |
|---|
