3.5. Уравнение прямой с угловым коэффициентом

Пусть — общее уравнение прямой на плоскости. Предположим, что . Тогда

ó ó , где , .

Исследуем геометрический смысл коэффициента .

Пусть и . Поскольку точки и принадлежат прямой , их координаты удовлетворяют ее уравнению:

, (5)

. (6)

Вычитая (5) из (6), имеем:

, где ,

(см. рис. 17).

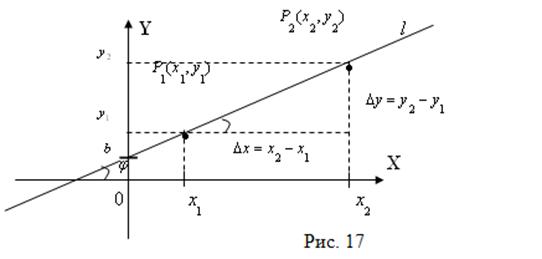
Таким образом, — Уравнение прямой на плоскости С угловым коэффициентом . Здесь:

— угол, который прямая образует с осью ,

— точка, в которой прямая пересекает ось ( ),

— координаты текущих точек прямой .

Пример 19. Пусть прямая задана общим уравнением: . Требуется написать ее уравнение с угловым коэффициентом.

Решение. Имеем: =.

Следовательно, угловой коэффициент равен . Очевидно,

— координаты точки, в которой прямая пересекает ось ,

— координаты точки, в которой прямая пересекает ось .

Пример 20. Описать свойства уравнений прямых на плоскости, параллельных оси .

Решение. В этом случае и . Если прямая задана своим общим уравнением , то

;

Но .

Таким образом, общее уравнение любой прямой, параллельной оси , всегда имеет вид

. (7)

Уравнение такой прямой с угловым коэффициентом имеет вид:

Итак, уравнение вида (или, в общем виде, ) на плоскости описывает прямую, параллельную оси и пересекающую ось в точке .

Пример 21. Описать свойства уравнений прямых на плоскости, параллельных оси .

Решение. В этом случае и . Если прямая задана своим общим уравнением , то

;

Но .

Таким образом, общее уравнение любой прямой, параллельной оси , всегда имеет вид

. (8)

Это уравнение эквивалентно уравнению вида

Где .

Пример 22. Четыре прямые заданы своими общими уравнениями:

: , : , : , : .

Требуется описать взаимное расположение прямой с прямыми , и .

Решение. Прямые и пересекаются, так как существует общая точка этих прямых, координаты которой удовлетворяют уравнениям данных прямых:

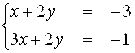
Пара координат точки пересечения является единственным решением этой системы.

Ответ 1: — координаты точки пересечения прямых и .

Ответ 2: Прямые и параллельны.

Действительно, система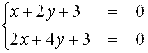

Не имеет решений (прямые и не имеют общих точек):

: ó =,

: ó =;

и — параллельны, так как не пересекаются и имеют равные угловые коэффициенты: .

Ответ 3: Прямые и совпадают.

Действительно, система

Имеет бесконечное множество решений, так как состоит из двух эквивалентных уравнений:

: ó =,

: ó =.

Оба уравнения описывают одну и ту же прямую.

Полезно отметить, что справедливо следующее

Утверждение 9. Если две прямые заданы своими общими уравнениями и , то могут представиться три случая:

1) — прямые имеют одну общую точку;

2) — прямые параллельны;

3) 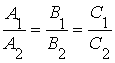— прямые совпадают.

Угол между прямыми (через угловые коэффициенты)

Пусть прямые и заданы своими уравнениями с угловыми коэффициентами (см. рис. 18):

: и : ,

Где = и = .

Очевидно, ó . Следовательно,

= = = . (9)

Условие параллельности двух прямых

= 0 ó = = 0 ó =

Условие перпендикулярности двух прямых

= ó = = 0 ó 1 + = 0 ó =

Уравнение прямой, проходящей через данную Точку с заданным угловым коэффициентом

Пусть на плоскости дана точка . Составим уравнение прямой, проходящей через эту точку под заданным углом к оси (см. рис. 19).

Напомним, что — угловой коэффициент прямой. Пусть — произвольная текущая точка прямой . Имеем

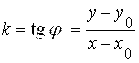
Итак, — Уравнение прямой на плоскости, проходящей через точку с угловым коэффициентом (здесь переменные — координаты текущих точек прямой).

Пример 23. Составить уравнение прямой, проходящей через точку под заданным углом к оси .

Решение. Искомое уравнение имеет вид

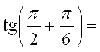
Где , , . Следовательно,

ó ó .

Ответ: — общее уравнение прямой;

— уравнение прямой с угловым коэффициентом.

< Предыдущая		Следующая >