3.4. Расстояние от точки до прямой на плоскости
Пусть дана прямая ![]() :
: ![]() , где
, где ![]() — ее нормальный вектор, и пусть точка
— ее нормальный вектор, и пусть точка ![]()
![]()
![]() , т. е.
, т. е. ![]() . Требуется определить расстояние от точки
. Требуется определить расстояние от точки ![]() до прямой
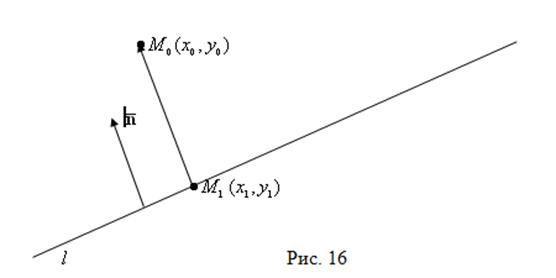
до прямой ![]() (см. рис. 16).
(см. рис. 16).
Пусть ![]() — ортогональная проекция точки
— ортогональная проекция точки ![]() на прямую
на прямую ![]() . Тогда
. Тогда
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Очевидно, ![]() = {
= {![]()
![]() ,
,![]()
![]() }. Отсюда
}. Отсюда
![]()
![]()
![]()
![]()
![]()
![]()
![]() или
или ![]()
![]()
![]() .
.
Напомним, что (![]() ,
,![]() ) =
) = ![]()
![]()
![]()
![]() , где
, где ![]() — угол между векторами
— угол между векторами ![]() и
и ![]() ; здесь
; здесь
![]()
![]() =
= 
Отсюда
(![]() ,
,![]() ) =
) = ![]()
![]() и |(
и |(![]() ,
,![]() )| =
)| = ![]()
![]() .
.
Следовательно,
![]() =
=  =
=  =
=
 =
=  .
.
Таким образом, расстояние ![]() от точки
от точки ![]() до прямой
до прямой ![]() находится по формуле
находится по формуле
![]() =
= ![]() =
=  . (3)
. (3)
Найдем теперь расстояние от начала координат ![]() до прямой
до прямой ![]() :
:
![]() =
= 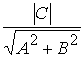 . (4)
. (4)
Пример 18. Найти расстояния от точки ![]() и от начала координат до прямой
и от начала координат до прямой ![]() :
: ![]() .
.
Решение. Имеем ![]() =
=  , где
, где ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Отсюда
. Отсюда
![]() =
= 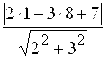 =
= ![]() .
.
Расстояние от начала координат до данной прямой:
![]() =
= 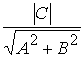 =
= ![]() .
.
| < Предыдущая | Следующая > |
|---|