Глава 31. Фундаментальные циклы и разрезы

Циклы и коциклы

Цикл может входить только в одну компоненту связности графа, поэтому далее без ограничения общности граф считается связным. Цикл (простой) рассматри­вается как множество ребер.

Разрезом Связного графа называется множество ребер, удаление которых делает граф несвязным. Простым Разрезом называется минимальный разрез, то есть такой, никакое собственное подмножество которого разрезом не является.

Здесь рассматриваются только простые циклы и разрезы, далее слово «простые» опускается.

Между циклами и разрезами существует определенная двойственность, поэтому разрезы иногда называют Коциклами.

Независимые множества циклов и коциклов

Рассмотрим операцию Å сложения по модулю 2 или симметрической разности над множествами ребер:

Множество М Называется Зависимым или Линейной комбинацией Множеств {Mi}ni=1, если

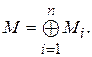
Множество циклов {ZI}ni=1 называется Независимым, Если ни один из циклов ZI не является линейной комбинацией остальных.

Множество разрезов {SI}ni=1 называется Независимым, Если ни один из разрезов SI не является линейной комбинацией остальных.

Циклический и коциклический ранг

Максимальное независимое множество циклов (или минимальное множество ци­клов, от которых зависят все остальные) называется Фундаментальной системой циклов. Циклы фундаментальной системы называются Фундаментальными, А ко­личество циклов в (данной) фундаментальной системе называется Циклическим рангом, Или Цикломатическим числом, Графа G И обозначается M(G). Максималь­ное независимое множество коциклов (разрезов) (или минимальное множество коциклов, от которых зависят все остальные) называется Фундаментальной си­стемой коциклов (разрезов). Коциклы (разрезы) фундаментальной системы назы­ваются Фундаментальными, А количество коциклов в (данной) фундаментальной системе называется Коциклическим рангом, Или Коцикломатическим числом, Графа G И обозначается M*(G).

Пусть T(V, ET) — Остов графа G(V, T). Кодеревом T*(V, E*T) остова Т называется остовный подграф, такой что E*T = Е \ ET. (Кодерево не является деревом!) Ребра кодерева называются Хордами Остова.

ТЕОРЕМА Если G — связный граф, то

M(G) = Q – P + 1, M*(G)= P – 1.

Эйлеров цикл

Если граф имеет цикл (не обязательно простой), содержащий все ребра графа по одному разу, то такой цикл называется Эйлеровым Циклом, а граф называется Эйлеровым Графом. Если граф имеет цепь (не обязательно простую), содержащую все вершины по одному разу, то такая цепь называется Эйлеровой Цепью, а граф называется Полуэйлеровым Графом.

Эйлеров цикл содержит не только все ребра (по одному разу), но и все вершины графа (возможно, по несколько раз). Ясно, что эйлеровым может быть только связный граф.

ТЕОРЕМА Если граф G связен и нетривиален, то следующие утверждения эквивалентны:

G — эйлеров граф;

Каждая вершина G имеет четную степень;

Множество ребер G можно разбить на простые циклы.

Гамильтонов цикл

Если граф имеет простой цикл, содержащий все вершины графа (по одному ра­зу), то такой цикл называется Гамильтоновым Циклом, а граф называется Гамильтоновым Графом.

Гамильтонов цикл не обязательно содержит все ребра графа. Ясно, что гамильтоновым может быть только связный граф.

ТЕОРЕМА (Дирак) Если в графе G(V, E) " U Î V D(V) ³ Р/2, то граф G является гамильтоновым.

Упражнения

1. Нарисовать диаграммы всех деревьев с 7 вершинами.

2. Допустим, что в ордереве все узлы, кроме листьев, имеют одну и ту же по­лустепень исхода N. В этом случае говорят, что дерево имеет постоянную Ширину ветвления п. Оценить высоту H Ордерева, которое имеет Р Узлов и постоянную ширину ветвления N.

< Предыдущая		Следующая >