Глава 30. Ориентированные, упорядоченные и бинарные деревья
Ориентированные деревья
Ориентированным деревом (или Ордеревом, Или Корневым Деревом) называется орграф со следующими свойствами:
1. существует единственный узел, полустепень захода которого равна 0. Он называется Корнем Ордерева;
2. полустепень захода всех остальных узлов равна 1;
3. каждый узел достижим из корня.
Пример
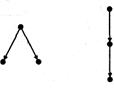
На рис. 7.3 приведены диаграммы всех различных ориентированных деревьев с 3 узлами, а на рис. 7.4 показаны диаграммы всех различных ориентированных деревьев с 4 узлами.
|
Рис. 7.3. Ориентированные деревья с 3 узлами |
Рис. 7.4. Ориентированные деревья с 4 узлами |
ТЕОРЕМА Ордерево обладает следующими свойствами:
1. Q = P – 1;
2. если в ордереве отменить ориентацию ребер, то получится свободное дерево;
3. в ордереве нет контуров;
4. Для каждого узла существует единственный путь, ведущий в этот узел из корня;
5. Подграф, определяемый множеством узлов, достижимых из узла v, является ордеревом с корнем v (это ордерево называется поддеревом узла v);
6. если в свободном дереве любую вершину назначить корнем, то получится ордерево.
Упорядоченные деревья
Множества Т1, ... , Tk В эквивалентном определении ордерева являются поддеревьями. Если относительный порядок поддеревьев T1, ... , Tk Фиксирован, то ордерево называется Упорядоченным.
Пример
Ориентированные и упорядоченные ориентированные деревья интенсивно используются в программировании. Выражения для представления выражений языков программирования, как правило, используются ориентированные упорядоченные деревья.
Бинарные деревья
Бинарное дерево — Это конечное множество узлов, которое либо пусто, либо состоит из корня и двух непересекающихся бинарных деревьев — левого и правого.
Бинарное дерево Не является Упорядоченным ордеревом.
Пример
На рис. 7.5 приведены две диаграммы деревьев, которые изоморфны как упорядоченные, ориентированные и свободные деревья, но не изоморфны как бинарные деревья.
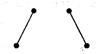
Рис. 7.5. Два различных бинарных дерева
Выровненные деревья
Ордерево называется Выровненным, Если все узлы, степень которых меньше 1 располагаются на одном или двух последних уровнях. Выровненное дерево имеет наименьшую возможную для данного Р Высоту H.
Пример
На рис. 7.6 приведены диаграммы выровненного (слева) и невыровненне: (справа) деревьев.
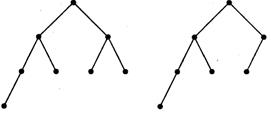
Рис. 7.6. Выровненное (слева) и невыровненное деревья
Сбалансированные деревья
(Бинарное) дерево называется Подровненным деревом, Или АВЛ-деревом (Адель-сон-Вельский и Ландис, 1962), или Сбалансированным деревом, Если для любого узла высота левого и правого поддеревьев отличается не более чем на 1.
Пример
На рис. 7.7 приведена диаграмма максимально несимметричного сбалансированного дерева, в котором для всех узлов высота левого поддерева ровно на 1 больше высоты правого поддерева.
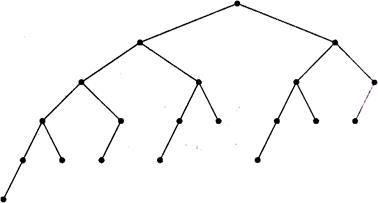
Рис. 7.7. Сбалансированное дерево
| < Предыдущая | Следующая > |
|---|