Глава 29. Деревья и циклы. Свободные деревья

Граф без циклов называется Ациклическим, Или Лесом. Связный ациклический граф называется (Свободным) деревом. Таким образом, компонентами связности леса являются деревья.

В связном графе G выполняется неравенство Q(G) ³ P(G)–1. Граф G, в котором Q(G) = P(G) - 1, называется Древовидным.

В ациклическом графе G Z(G) = 0. Пусть И, V — Несмежные вершины графа G, х = (И, V) Ï Е. Если граф G + х Имеет только один простой цикл, Z(G + х) = 1, То граф G Называется Субциклическим.

Пример

На рис. 7.1 показаны диаграммы всех различных (свободных) деревьев с 5 вер­шинами, а на рис. 7.2 — диаграммы всех различных (свободных) деревьев с 6 вершинами.

Рис. 7.1. Свободные деревья с 5 вершинами

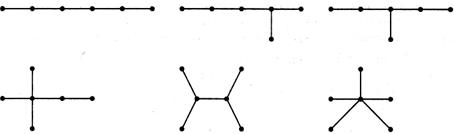
Рис. 7.2. Свободные деревья с 6 вершинами

< Предыдущая		Следующая >