Глава 28. Связность в орграфах

Сильная, односторонняя и слабая связность

В неориентированном графе две вершины либо связаны (если существует со­единяющая их цепь), либо не связаны. В ориентированном графе отношение связанности вершин несимметрично, а потому определение связности отличает­ся.

Пусть G(V, Е) — Орграф, V1 и V2 — Его вершины. Говорят, что две вершины V1 и V2 сильно связаны В орграфе G, Если существует путь (ориентированная цепь) из V1 в V2 и из V2 в V1. Говорят, что две вершины V1 И V2 Односторонне связаны В орграфе G, Если существует путь либо из V1 в V2, либо из V2 в V1. Говорят, что две вершины V1 и V2 Слабо связаны В орграфе G, Если они связаны в графе G', Полученном из G Отменой ориентации ребер. Если все вершины в орграфе силь­но (односторонне, слабо) связаны, то орграф называется сильно (односторонне, слабо) связным. Сильная связность влечет одностороннюю связность, которая влечет слабую связность. Обратное неверно.

Компоненты сильной связности

Компоненты сильной связности (КСС) орграфа G — Это его максимальные сильно связные подграфы.

Каждая вершина орграфа принадлежит только одной КСС. Если вершина не связана с другими, то считаем, что она сама образует КСС. Конденсацией G* Орграфа G (или Графом Герца, Или Фактор-графом) Называется орграф, который получается стягиванием в одну вершину каждой КСС орграфа G.

Пример

На рис. 6.3 показаны диаграммы орграфа и его конденсации.

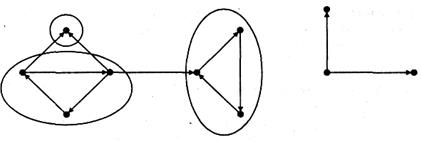
Рис. 6.3 Орграф (слева) и его фактор-граф (справа)

Упражнения

1. Построить пример графов G1 и G2, для которых P1 = P2, Q1 = Q2, D1 = D2, D1 = D2, Но G1~G2.

2. Построить граф по матрице смежности:

.

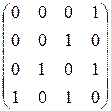8. Построить граф по матрице смежности:

.

9. Построить граф по матрице инцидентности:

.

10. Построить граф по матрице инцидентности:

.

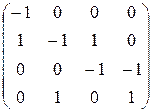11. Построить граф по списку пар вершин: ({1,4}, {2,4}, {1,2}, {2,4}).

12. Построить граф по списку пар вершин: ((2,2), (4,1), (4,2), (3,4)).

13. Построить неориентированный граф по списку списков: ((2,4,5), (1,4), (4), (1,2,3), (2)).

14. Построить орграф по списку списков: ((2,1), (2,4), (4,3), Æ, (2,3,4)).

< Предыдущая		Следующая >