Глава 11. Принцип включения и исключения

Объединение конфигураций

Часто комбинаторная конфигурация является объединением других, число ком­бинаций в которых вычислить проще. В таком случае требуется уметь вычислять число комбинаций в объединении. В простых случаях формулы для вычисления очевидны:

|AB|=|A|+|B|-|AB|,

|ABC|=|A|+|B|+|C|-|AB|-|BC|-|AC|+|ABC|

Пример

Сколько существует натуральных чисел, меньших 1000, которые не делятся ни на 3, ни на 5, ни на 7? Всего чисел, меньших тысячи, 999. Из них:

999 : 3 = 333 делятся на 3,

999 : 5 = 199 делятся на 5,

999 : 7 = 142 делятся на 7,

999 : (3 * 5) = 66 делятся на 3 и на 5,

999 : (3 * 7) = 47 делятся на 3 и на 7,

999 : (5 * 7) = 28 делятся на 5 и на 7,

999 : (3 * 5 * 7) = 9 делятся на 3, на 5 и на 7.

Имеем: 999 – (333 + 199 + 142 – 66 – 47 – 28 + 9) = 457.

Принцип включения и исключения

Следующая формула, известная как Принцип включения и исключения, Позволя­ет вычислить мощность объединения множеств, если известны их мощности и мощности всех пересечений.

ТЕОРЕМА

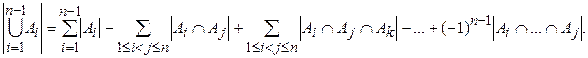
< Предыдущая		Следующая >