Глава 12. Производящие функции

Основная идея

Пусть есть последовательность комбинаторных чисел АI И последовательность функций J I (X). Рассмотрим формальный ряд:

F(X) =

F(X) называется Производящей функцией (для заданной последовательности ком­бинаторных чисел Ai Относительно заданной последовательности функций J I (X).

Обычно используют J I (X) = хi Или J I (X) = Xi/I!.

Пример

Из формулы бинома Ньютона при У = 1 имеем:

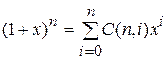
Таким образом, (1+х)П Является производящей функцией для биномиальных коэффициентов.

Метод неопределенных коэффициентов

Из математического анализа известно, что если

F(X) = и F (X) =

То "I аI = Bi (для рассматриваемых здесь систем функций J I ).

В качестве примера применения производящих функций рассмотрим доказатель­ство следующего тождества.

ТЕОРЕМА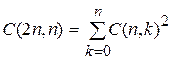

Доказательство

Имеем: (1 + х)2п = (1 + х)П(1 + X) п. Следовательно,

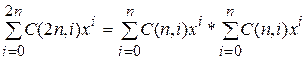
Приравняем коэффициент при Хп:

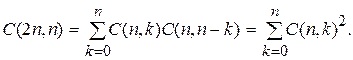
Упражнения

1. Определить , .

2. Получить всевозможные комбинации перестановок множества {A,B,C}.

3. Получить всевозможные размещения и сочетания двух элементов множества {A,B,C}.

4. В мешке два красных, три синих и один белый шар. Сколькими способами можно вынуть цветной шар.

5. В одном мешке два красных, три синих и один белый шар, в другом три красных, пять синих и один черный шар. Сколькими способами можно вынуть два синих шара из двух мешков.

6. Доказать, что А(Т, п) = А(Т - 1, п) + пА(Т - 1, п - 1).

7. Доказать, что MC(Т - 1, п - 1) = ПС(Т, п).

< Предыдущая		Следующая >