Глава 10. Комбинаторика. Комбинаторные конфигурации

Во многих практических случаях возникает необходимость подсчитать количе­ство возможных комбинаций объектов, удовлетворяющих определенным усло­виям. Такие задачи называются Комбинаторными. Разнообразие комбинаторных задач не поддается исчерпывающему описанию, но среди них есть целый ряд особенно часто встречающихся, для которых известны способы подсчета.

Размещения

Число всех функций (при отсутствии ограничений), или число всех возможных способов разместить П Предметов по Т Ящикам называется, Числом размещений И обозначается U(M,N).

ТЕОРЕМА U(Т, п)= Mn

Доказательство

Каждый из N предметов можно разместить M способами.

Пример

При игре в кости бросаются две кости и выпавшие на верхних гранях очки скла­дываются. Какова вероятность выбросить 12 очков? Каждый возможный исход соответствует функции F: {1,2}® {1,2,3,4,5,6} (аргумент — номер кости, ре­зультат — очки на верхней грани). Таким образом, всего возможно U(6,2) = 62 = 36 различных исходов. Из них только один (6 + 6) дает двенадцать очков. Вероятность 1/36.

Размещения без повторений

Число инъективных функций, или число всех возможных способов разместить П Предметов по M ящикам, не более чем по одному в ящик, называется Числом размещений без повторений И обозначается А(M, п) или [M]n, или (M)n.

ТЕОРЕМА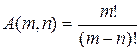

Доказательство

Ящик для первого предмета можно выбрать M способами, для второго — M - 1 способами, и т. д. Таким образом,

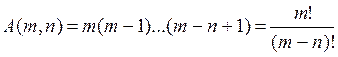
По определению считают, что А(Т, N) = 0 при П > Т И А(Т, 0) = 1.

Пример

В некоторых видах спортивных соревнований исходом является определение участников, занявших первое, второе и третье места. Сколько возможно раз­личных исходов, если в соревновании участвуют П Участников? Каждый воз­можный исход соответствует функции F: {1,2,3} ® {1..N} (аргумент — номер призового места, результат — номер участника). Таким образом, всего возможно А(П,3) = П(П - 1)(N - 2) различных исходов.

Перестановки

Число взаимнооднозначных функций, или Число перестановок п Предметов, обо­значается Р(П).

ТЕОРЕМА Р(N) = N!

Доказательство

Р(N) = А(N, N) = N(N - 1)…(N - N + 1)= N(N - 1)...1 = N!.

Пример

Последовательность E = (E1,...,Em) непустых подмножеств множества Е (E Ì 2E, Ei Ì Е, Ei ¹ Æ) называется Цепочкой В Е, Если

"IÎ1..M - 1 Ei Ì Ei+1 & Ei ¹ Ei+1.

Цепочка E называется Полной Цепочкой в Е, Если |E| = |Е|. Сколько существует полных цепочек? Очевидно, что в полной цепочке каждое следующее подмноже­ство Ei+1 получено из предыдущего подмножества Ei Добавлением ровно одного элемента из Е И, таким образом, |E1| = 1, |E2| = 2, ..., |Ет| = |Е| = т. Следова­тельно, полная цепочка определяется порядком, в котором элементы Е Добавля­ются для образования очередного элемента полной цепочки. Отсюда количество полных цепочек — это количество перестановок элементов множества Е, Рав­ное M!.

Сочетания

Число строго монотонных функций, или число размещений П Неразличимых предметов по Т Ящикам, не более чем по одному в ящик, то есть число способов выбрать из m ящиков N ящиков с предметами, называется Числом сочетаний И обозначается С(Т, п) или или .

ТЕОРЕМА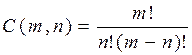

Доказательство

1. Число размещений без повторений нужно разделить на число перестановок, поскольку предметы неразличимы.

2. Число сочетаний является числом строго монотонных функций, потому что строго монотонная функция F: 1..п ® L..M определяется набором своих значений, причем 1£ F(1)< … < F(N) £ M. Другими словами, каждая строго монотонная функция определяется выбором N чисел из диапазона 1..m. Таким образом, число строго монотонных функций равно числу N-элементных подмножеств M-элементного множества, которое, в свою очередь, равно числу способов выбрать N Ящиков с предметами из M ящиков.

По определению С (M, N) = 0 при N > M.

Пример

В начале игры в домино каждому играющему выдается 7 костей из имеющихся 28 различных костей. Сколько существует различных комбинаций костей, которые игрок может получить в начале игры? Очевидно, что искомое число равно числу 7-элементных подмножеств 28-элементного множества. Имеем:

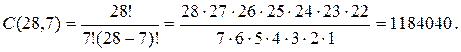
Сочетания с повторениями

Число монотонных функций, или число размещений N неразличимых предме­тов по M ящикам, называется Числом сочетаний с повторениями И обозначается V(M, N).

ТЕОРЕМА V(M, N)=C(N + M - 1, N).

Пример

Сколькими способами можно рассадить N Вновь прибывших гостей среди M Го­стей, уже сидящих за круглым столом? Очевидно, что между то сидящими за круглым столом гостями имеется M Промежутков, в которые можно рассаживать вновь прибывших. Таким образом, это можно сделать

Способами.

< Предыдущая		Следующая >