7.3. Правая часть в виде произведения полинома и экспоненты
Пусть правая часть неоднородного линейного дифференциального уравнения с постоянными коэффициентами (7.1) имеет вид
![]() ,
,
Где ![]() – многочлен степени
– многочлен степени ![]() , то есть
, то есть
![]() ,
,
А ![]() – некоторое число. Тогда уравнение (7.1) примет вид
– некоторое число. Тогда уравнение (7.1) примет вид
![]() . (7.6)
. (7.6)
Положим ![]() , где
, где ![]() – новая неизвестная функция. Обозначим левую часть уравнения (7.6) через
– новая неизвестная функция. Обозначим левую часть уравнения (7.6) через ![]() , а левую часть соответствующего ему характеристического уравнения – через
, а левую часть соответствующего ему характеристического уравнения – через ![]() . Тогда по формуле (3.8) линейного дифференциального оператора для произведения функций получим
. Тогда по формуле (3.8) линейного дифференциального оператора для произведения функций получим
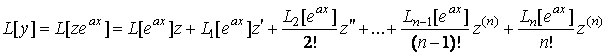 .
.
В силу определения линейного дифференциального оператора (3.4) имеем:
![]() ,
, ![]() ,
, ![]() , …,
, …,
![]() ,
, ![]() .
.
Следовательно,
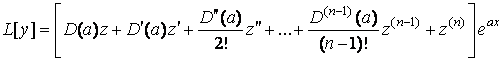 .
.
Поэтому, подставляя ![]() в уравнение (7.6), получим
в уравнение (7.6), получим
 .
.
Сокращая это равенство на ![]() , имеем
, имеем
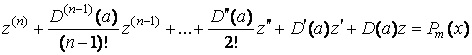 . (7.7)
. (7.7)
Получено неоднородное линейное дифференциальное уравнение с постоянными коэффициентами вида (7.2) с многочленом в правой части, которое рассмотрено в предыдущем подразделе. При этом возможны два случая.
В первом случае предположим, ![]() , то есть значение
, то есть значение ![]() не является корнем характеристического уравнения. Тогда частное решение уравнения (7.7) ищется в виде (7.3)
не является корнем характеристического уравнения. Тогда частное решение уравнения (7.7) ищется в виде (7.3)
![]() .
.
Следовательно, частное решение исходного уравнения (7.6) нужно искать в виде
![]() . (7.8)
. (7.8)
Во втором случае пусть ![]() ,
, ![]() ,
, ![]() , …,
, …, ![]() , но
, но ![]() , то есть значение
, то есть значение ![]() является
является ![]() -кратным корнем характеристического уравнения. Тогда частное решение уравнения (7.7) ищется в виде (7.5)
-кратным корнем характеристического уравнения. Тогда частное решение уравнения (7.7) ищется в виде (7.5)
![]() .
.
Частное решение исходного уравнения (7.6) нужно искать в виде
![]() . (7.9)
. (7.9)
Можно условно считать, что в первом случае будет ![]() и из формулы (7.9) получается формула (7.8) как частный случай. То есть, можно условно считать первый случай частным случаем второго. В то же время, формулы (7.3) и (7.5) предыдущего подраздела теперь вытекают из формул (7.8) и (7.9) данного подраздела как частный случай при
и из формулы (7.9) получается формула (7.8) как частный случай. То есть, можно условно считать первый случай частным случаем второго. В то же время, формулы (7.3) и (7.5) предыдущего подраздела теперь вытекают из формул (7.8) и (7.9) данного подраздела как частный случай при ![]() .
.
Если в уравнении (7.1) правая часть есть сумма нескольких слагаемых вида
![]() ,
,
То можно для каждого слагаемого найти соответствующее частное решение, а затем на основании принципа суперпозиции сложить их.
Пример 7.3. Найти общее решение уравнения
![]() .
.
Решение. Характеристическое уравнение
![]()
Имеет корни ![]() ,
, ![]() . Запишем общее решение соответствующего однородного уравнения
. Запишем общее решение соответствующего однородного уравнения
![]() .
.
В данном случае правая часть исходного уравнения имеет вид
![]() .
.
Поскольку число ![]() не совпадает ни с
не совпадает ни с ![]() , ни с
, ни с ![]() , то частное решение ищем в виде
, то частное решение ищем в виде
![]() ,
,
То есть
![]() .
.
Для такого решения имеем:
![]() ,
, ![]() .
.
Подставляя ![]() ,
, ![]() и
и ![]() в исходное уравнение и сокращая его на
в исходное уравнение и сокращая его на ![]() , получим
, получим
![]() .
.
Приравнивая коэффициенты при одинаковых степенях ![]() и
и ![]() , имеем:
, имеем:
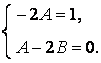
Отсюда ![]() ,
, ![]() . Итак, частное решение
. Итак, частное решение
 .
.
Складывая ![]() и
и ![]() , получим общее решение исходного уравнения
, получим общее решение исходного уравнения
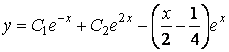 .
.
Пример 7.4. Найти общее решение уравнения
![]() .
.
Решение. Характеристическое уравнение
![]()
Имеет корни ![]() ,
, ![]() . Общее решение однородного уравнения
. Общее решение однородного уравнения
![]() .
.
Правая часть исходного уравнения имеет в данном случае вид
![]() ,
,
Где
![]() ,
, ![]() .
.
Значит
![]() ,
,
Где
![]() ,
, ![]() .
.
Итак, полагаем
![]() .
.
Дифференцируя эту функцию, имеем:
![]() ,
,
![]() ,
,
![]() .
.
Подставляя ![]() ,
, ![]() ,
, ![]() и
и ![]() в исходное уравнение, получим
в исходное уравнение, получим
![]()
![]() .
.
После упрощения имеем
![]() .
.
Приравнивая коэффициенты, получим:

Отсюда ![]() ,
, ![]() ,
, ![]() . Найдено частное решение
. Найдено частное решение
 .
.
Общее решение исходного уравнения
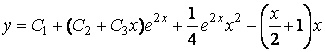 .
.
| < Предыдущая | Следующая > |
|---|