7.2. Уравнения с правой частью в виде полинома
Пусть правая часть неоднородного линейного дифференциального уравнения с постоянными коэффициентами (7.1) имеет вид
![]() ,
,
Где ![]() – многочлен степени
– многочлен степени ![]() , то есть
, то есть
![]() .
.
Тогда уравнение (7.1) примет вид
![]() . (7.2)
. (7.2)
Рассмотрим два случая.
В первом случае предположим, что в уравнении (7.1) ![]() . Тогда частное решение уравнения (7.2) можно искать в виде
. Тогда частное решение уравнения (7.2) можно искать в виде
![]() , (7.3)
, (7.3)
Где ![]() – некоторый многочлен степени
– некоторый многочлен степени ![]() . Действительно, в этом случае, положим
. Действительно, в этом случае, положим
![]() ,
,
Где ![]() – неизвестные коэффициенты. Дифференцируя это равенство, получим:
– неизвестные коэффициенты. Дифференцируя это равенство, получим:
![]() ,
,
![]() , … .
, … .
Подставляя эти производные в уравнение (7.2) и приравнивая коэффициенты в левой и правой частях полученного равенства при одинаковых степенях переменной ![]() –
– ![]() ,
, ![]() ,
, ![]() , …, будем иметь:
, …, будем иметь:

Из первого уравнения этой системы найдем ![]() , из второго –
, из второго – ![]() , из третьего –
, из третьего – ![]() и так далее. Поскольку коэффициент при каждой очередной неизвестной равен
и так далее. Поскольку коэффициент при каждой очередной неизвестной равен ![]() , а
, а ![]() , то числа
, то числа ![]() ,
, ![]() ,
, ![]() , …,
, …, ![]() из этой системы могут быть найдены и при том единственным образом.
из этой системы могут быть найдены и при том единственным образом.
Пример 7.1. Найти общее решение уравнения
![]() .
.
Решение. Характеристическое уравнение
![]()
Имеет корни ![]() ,
, ![]() . Следовательно, общее решение соответствующего однородного уравнения
. Следовательно, общее решение соответствующего однородного уравнения
![]() .
.
Правая часть исходного уравнения имеет в данном случае вид
![]() .
.
Поскольку ![]() , то частное решение ищем в виде
, то частное решение ищем в виде
![]() ,
,
То есть
![]() .
.
Для такого решения имеем:
![]() ,
, ![]() ,
, ![]() .
.
Подставляя ![]() ,
, ![]() ,
, ![]() и
и ![]() в исходное уравнение, получим
в исходное уравнение, получим
![]() .
.
Приравнивая коэффициенты при одинаковых степенях ![]() ,
, ![]() и
и ![]() , имеем:
, имеем:
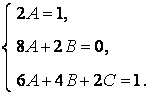
Отсюда
![]() ,
, ![]() ,
, ![]() .
.
Итак, частное решение
 .
.
Следовательно, общее решение исходного уравнения
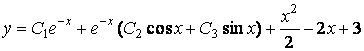 .
.
Во втором случае пусть ![]() и при этом
и при этом ![]() ,
, ![]() , …,
, …, ![]() , но
, но ![]() . Тогда уравнение (7.1) примет вид
. Тогда уравнение (7.1) примет вид
![]() . (7.4)
. (7.4)
Это дифференциальное уравнение, допускающее понижение порядка. Положим ![]() , где
, где ![]() – новая неизвестная функция. Получим для нее уравнение
– новая неизвестная функция. Получим для нее уравнение
![]() .
.
Поскольку ![]() , то мы пришли к первому случаю. Поэтому частное решение такого уравнения ищем в виде
, то мы пришли к первому случаю. Поэтому частное решение такого уравнения ищем в виде
![]() ,
,
Где ![]() – некоторый многочлен степени
– некоторый многочлен степени ![]() . Если его коэффициенты уже найдены, то для частного решения уравнения (7.4) имеем
. Если его коэффициенты уже найдены, то для частного решения уравнения (7.4) имеем
![]() .
.
Интегрируя это равенство ![]() раз подряд, получим
раз подряд, получим
![]()
![]() .
.
Здесь ![]() ,
, ![]() , …,
, …, ![]() – некоторые определенные числа, а
– некоторые определенные числа, а ![]() ,
, ![]() , …,
, …, ![]() –произвольные постоянные. Поскольку мы ищем произвольное частное решение уравнения (7.4), то можно положить
–произвольные постоянные. Поскольку мы ищем произвольное частное решение уравнения (7.4), то можно положить ![]() , и тогда получим
, и тогда получим
![]() .
.
Итак, в этом случае
![]() , (7.5)
, (7.5)
Где ![]() – некоторый многочлен степени
– некоторый многочлен степени ![]() .
.
Примечание. Из дифференциального уравнения (7.4) следует, что характеристическое уравнение для второго случая имеет вид
![]() .
.
Отсюда следует, что корень этого уравнения ![]() имеет кратность
имеет кратность ![]() . Именно в этом случае равенство (7.5) отличается от (7.3) появлением справа сомножителя
. Именно в этом случае равенство (7.5) отличается от (7.3) появлением справа сомножителя ![]() в частном решении. Первый случай может рассматриваться как частный случай второго случая при
в частном решении. Первый случай может рассматриваться как частный случай второго случая при ![]() . Тогда формула (7.5) превращается в (7.3).
. Тогда формула (7.5) превращается в (7.3).
Пример 7.2. Найти общее решение уравнения
![]() .
.
Решение. Характеристическое уравнение
![]()
Имеет корни ![]() ,
, ![]() . Следовательно, общее решение соответствующего однородного уравнения
. Следовательно, общее решение соответствующего однородного уравнения
![]() .
.
Правая часть исходного уравнения имеет в данном случае вид
![]() .
.
Поскольку ![]() , то частное решение ищем в виде
, то частное решение ищем в виде
![]() ,
,
То есть
![]() ,
, ![]() .
.
Для такого решения имеем:
![]() ,
, ![]() ,
, ![]() .
.
Подставляя ![]() ,
, ![]() ,
, ![]() и
и ![]() в исходное уравнение, получим
в исходное уравнение, получим
![]() .
.
Приравнивая коэффициенты при одинаковых степенях ![]() и
и ![]() , имеем:
, имеем:
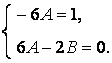
Отсюда ![]() ,
, ![]() . Итак, частное решение
. Итак, частное решение
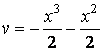 .
.
Складывая ![]() и
и ![]() , получим общее решение исходного уравнения
, получим общее решение исходного уравнения
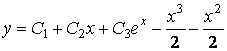 .
.
| < Предыдущая | Следующая > |
|---|