6.1. Общие теоремы о неоднородных линейных уравнениях

Рассмотрим неоднородное линейное дифференциальное уравнение

. (6.1)

С использованием линейного дифференциального оператора представим это уравнение в сокращенной записи

. (6.2)

Докажем две общие теоремы для решений такого уравнения.

Теорема 1. Если функции , , …, являются решениями уравнений , , …, , то функция

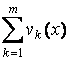
Удовлетворяет уравнению

.

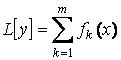Доказательство. Действительно, по условию

, , …, .

Складывая эти тождества, получим

.

По свойству линейности дифференциального оператора

.

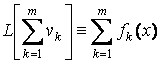Доказанную теорему называют принципом суперпозиции решений.

Теорема 2. Если комплекснозначная функция является решением уравнения с комплекснозначной правой частью

,

То функции и являются решениями уравнений

, .

Доказательство. По условию

.

По свойству линейности дифференциального оператора

.

Приравнивая в этом тождестве вещественные и мнимые части, получим

, ,

Что и требовалось доказать.

Очевидно, что доказанные свойства решений неоднородного линейного дифференциального уравнения вытекают из свойств линейного дифференциального оператора . Поэтому их можно назвать свойствами линейности решений неоднородных линейных уравнений.

< Предыдущая		Следующая >