5.4. Случай кратных вещественных корней

Пусть все корни характеристического уравнения (5.2) вещественные, но среди них имеются кратные. Обозначим через , , …, различные корни. Им отвечают частных решений линейного дифференциального уравнения (5.1):

, , …, .

Эти решения линейно независимы, но поскольку их число , они не образуют фундаментальную систему решений. Дополнить эти решения до фундаментальной системы позволяет следующая лемма.

Лемма. Если число является корнем характеристического уравнения (5.2) кратности , то функция при любом значении является решением Линейного дифференциального уравнения (5.1).

Доказательство. По формуле (3.8) линейного дифференциального оператора для произведения функций имеем

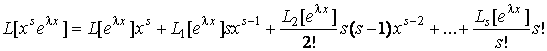Здесь – левая часть линейного дифференциального уравнения (5.1). Обозначим через левую часть характеристического уравнения (5.2). Тогда в силу определения линейного дифференциального оператора (3.4) имеем:

, , , …,

, .

Поэтому

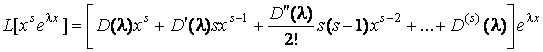Поскольку , то есть меньше кратности корня характеристического многочлена , то

, , , …, .

Следовательно, , что и доказывает лемму.

Итак, если – -кратный корень характеристического уравнения (5.2), то ему отвечают частных решений дифференциального уравнения (5.1):

, , , , .

Предположим теперь, что характеристическое уравнение (5.2) имеет корень кратности , корень кратности , …, корень кратности . Очевидно, что . Тогда получим частные решения:

(5.4)

Докажем утверждение, что эти решений линейно независимы. Предположим противное, то есть что функции (5.4) линейно зависимы. Тогда имеет место тождество

Где среди чисел , , …, , , , …, , …, , , …, не все равны нулю. Перепишем последнее тождество в виде

, (5.5)

Где , , …, – многочлены, степени которых не превосходят , , …, соответственно, причем ни один из этих многочленов не равен тождественно нулю.

Разделим тождество (5.5) на . Получим

. (5.6)

Будем дифференцировать это тождество нужное число раз. Так как для любого многочлена и любого числа будет

Где – многочлен той же степени, что и , то после -кратного дифференцирования тождества (5.6) имеем

. (5.7)

При этом, поскольку степени многочленов , , …, совпадают со степенями многочленов , , …, , то каждый из многочленов , , …, не равен нулю.

Разделим тождество (5.7) на и получим

Дифференцируя это тождество раз, имеем

Разделим это на и полученное тождество продифференцируем раз. Продолжая этот процесс, в результате получим тождество

Где – многочлен той же степени, что и , не равный тождественно нулю. Но тогда последнее тождество приводит к противоречию, которое и доказывает требуемое утверждение.