5.3. Случай простых комплексных корней

Пусть корни характеристического уравнения (5.2) , , …, различны, но среди них имеются комплексные корни. Поскольку все коэффициенты , , …, этого уравнения вещественны, то это уравнение, имея комплексный корень , в то же время имеет и комплексно-сопряжённый ему корень , где . Пусть, например, , , а остальные корни уравнения (5.2) , , …, вещественные. Тогда кроме частных решений линейного дифференциального уравнения (5.1)

, , …,

Имеем еще два комплекснозначных его решения:

, .

На основе этих двух решений введем функции

, .

С одной стороны, эти функции являются решениями линейного дифференциального уравнения (5.1) как линейные комбинации его решений. С другой стороны, согласно формулам Эйлера,

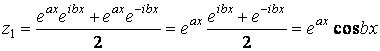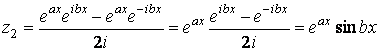Поэтому и – вещественные функции. Докажем, что решения , , , , …, образуют фундаментальную систему решений. Эта система функций получена из исходной фундаментальной системы решений путем линейного преобразования

Определитель матрицы этого преобразования равен

Следовательно, данное линейное преобразование неособенное, а, значит, система функций , , , , …, действительно образует фундаментальную систему решений. Поэтому общее решение линейного дифференциального уравнения (5.1) в этом случае можно записать в виде

Если среди корней характеристического уравнения (5.2) , , …, имеется несколько пар комплексно-сопряжённых корней, то каждой паре отвечает в общем решении линейного уравнения (5.1) пара слагаемых