4.2. Фундаментальная система решений однородных уравнений

Рассмотрим однородное линейное дифференциальное уравнение -го порядка

. (4.2)

Система линейно независимых решений уравнения (4.2) , , …, называется Фундаментальной системой решений.

Теорема 1. Любое однородное линейное Дифференциальное уравнение имеет фундаментальную систему решений.

Доказательство. Возьмем и рассмотрим различных наборов начальных условий:

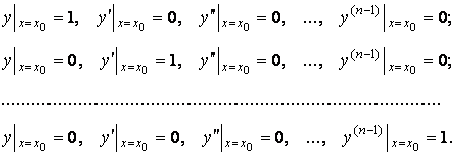
Эти наборы начальных условий соответствует некоторым решениям уравнения (4.2) . Покажем, что эти решения линейно независимы. В силу начальных условий вронскиан решений имеет вид

Поскольку , то рассмотренные функции линейно независимы, поэтому образуют фундаментальную систему решений.

Примечание. Из доказательства теоремы очевидно, что для уравнения (4.2) существует бесчисленное множество фундаментальных систем решений.

Теорема 2. Любое неособенное линейное преобразование фундаментальной системы решений однородного линейного Дифференциального уравнения образует фундаментальную систему решений.

Доказательство. Пусть – фундаментальная система решений уравнения (4.2). С помощью линейного преобразования получим новую систему функций:

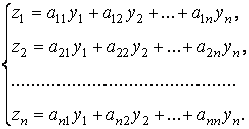
Здесь – некоторые числа. Пусть матрица такого преобразования

Поскольку по условию теоремы преобразование неособенное, то .

Докажем, что функции , , …, образуют фундаментальную систему решений. То, что эти функции являются решениями уравнения (4.2), вытекает из следствия основных теорем 1 и 2 для однородных линейных дифференциальных уравнений из предыдущего подраздела. Докажем, что эти решения линейно независимы. Составим вронскиан для новой системы функций