4.1. Общие теоремы об однородных линейных уравнениях

Рассмотрим однородное линейное дифференциальное уравнение (3.2), которое с обозначением линейного дифференциального оператора (3.4) можно представить в виде (3.7), то есть . Общие свойства решений такого уравнения даны в следующих теоремах.

Теорема 1. Если функции и являются решениями однородного линейного Дифференциального уравнения, то и сумма функций также является решением этого уравнения.

Доказательство. По условию теоремы и . В силу свойства аддитивности линейного дифференциального оператора

.

Теорема 2. Если функция является решением однородного линейного Дифференциального уравнения, а – произвольная постоянная, то и функция является решением.

Доказательство. По определению решения . По свойству однородности линейного дифференциального оператора . Отсюда следует, – решение линейного однородного уравнения.

Следствие. Если функции , , …, являются решениями однородного линейного Дифференциального уравнения, то и любая линейная комбинация этих функций является решением, то есть решением является функция

.

Доказательство. Применяя линейный дифференциальный оператор к функции и пользуясь теоремами 1 и 2, получим

,

Откуда и следует, что есть решение уравнения.

Теорема 3. Если система решений , , …, однородного линейного Дифференциального уравнения линейно независима, то вронскиан этой системы ни при одном значении переменной не обращается в нуль.

Доказательство. Предположим противное, то есть что существует такое , что вронскиан системы решений обращается в нуль и . Составим систему равенств

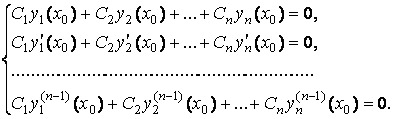(4.1)

Определитель этой системы равен , а значит, по предположению он равен нулю

.

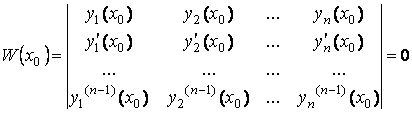Тогда однородная система линейных алгебраических уравнений (4.1) имеет ненулевые решения. Пусть , , …, – одно из них. Составим по нему функцию

.

По следствию теорем 1 и 2 функция также является решением однородного линейного уравнения. Равенства (4.1), в которых числа заменены на , означают, что функция удовлетворяет нулевым начальным условиям:

, , …, .

Но функция также удовлетворяет и уравнению , и нулевым начальным условиям. В силу единственности решения заключаем, что , то есть и

.

Поскольку есть линейная комбинация системы решений , , …, , причём существуют коэффициенты , то эта система решений является линейно зависимой, что противоречит условию теоремы. Полученное противоречие и доказывает теорему.

Теорема 3 имеет два следствия.

Следствие 1. Если , , …, являются решениями линейного однородного уравнения, то их вронскиан либо не обращается в нуль ни в одной точке, либо тождественно равен нулю.

Действительно, если эта система функций линейно независима, то вронскиан по теореме 3. Если же эти функции линейно зависимы, то по необходимому условию линейной зависимости .

Следствие 2. Для того, чтобы решения , , …, однородного линейного дифференциального уравнения были линейно независимы, необходимо и достаточно, чтобы их вронскиан ни в одной точке не обращался бы в нуль.

< Предыдущая		Следующая >