3.4. Линейно зависимые и линейно независимые функциИ
Пусть имеется система функций ![]() ,
, ![]() , …,
, …, ![]() , определенных на некотором интервале
, определенных на некотором интервале ![]() .
.
Функции ![]() ,
, ![]() , …,
, …, ![]() , заданные на интервале
, заданные на интервале ![]() , называются Линейно зависимыми, если существуют такие числа
, называются Линейно зависимыми, если существуют такие числа ![]() ,
, ![]() , …,
, …, ![]() , не все равные нулю, что для всех
, не все равные нулю, что для всех ![]() будет
будет
![]() . (3.9)
. (3.9)
Пусть для определённости ![]() . Тогда из (3.9) имеем
. Тогда из (3.9) имеем
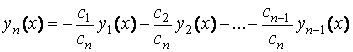 ,
,
То есть ![]() – линейная комбинация функций
– линейная комбинация функций ![]() ,
, ![]() , …,
, …, ![]() .
.
Обратно, пусть
![]() .
.
Тогда
![]()
Для всех рассматриваемых ![]() . Значит функции
. Значит функции ![]() ,
, ![]() , …,
, …, ![]() линейно зависимые.
линейно зависимые.
Итак, система функций является линейно зависимой тогда и только тогда, когда одна из них является линейной комбинацией остальных.
Если же тождество (3.9) имеет место тогда и только тогда, когда ![]() , то функции
, то функции ![]() ,
, ![]() , …,
, …, ![]() называются Линейно независимыми.
называются Линейно независимыми.
Пример 3.1. Пусть ![]() ,
, ![]() ,
, ![]() .
.
Имеем
![]() ,
,
То есть
![]() .
.
Следовательно, функции ![]() ,
, ![]() ,
, ![]() линейно зависимые на любом интервале
линейно зависимые на любом интервале ![]() .
.
Пример 3.2. Покажем, что функции 1, ![]() ,
, ![]() , …,
, …, ![]() линейно независимы. Для них тождество (3.9) запишется так:
линейно независимы. Для них тождество (3.9) запишется так:
![]() . (3.10)
. (3.10)
Но многочлен тождественно равен нулю тогда и только тогда, когда равны нулю все его коэффициенты. А значит из (3.10) следует, что ![]() , что и требовалось доказать.
, что и требовалось доказать.
| < Предыдущая | Следующая > |
|---|