3.3. Линейный дифференциальный оператор произведения функций

Докажем еще одно свойство линейного дифференциального оператора для произведения функций.

Правую часть линейного дифференциального оператора , представленного равенством (3.5), формально продифференцируем как многочлен по аргументу и получим оператор

.

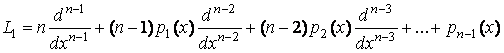Точно так же продифференцируем правую часть этого оператора и получим оператор

.

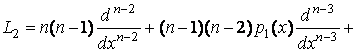
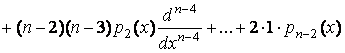Продолжая этот процесс, получим операторы:

,

.

Теорема. Для любых раз дифференцируемых функций и имеет место равенство

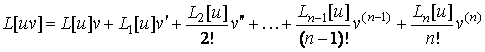, (3.8)

Где

,

,

,

.

Доказательство. Используя формулу Лейбница для производных произведения двух функций, имеем:

,

,

,

.

Умножим эти равенства соответственно на , , , …, 1 и сложим:

.

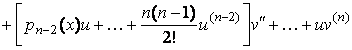Изменяя порядок слагаемых в квадратных скобках и используя операторы , , , …, , получим формулу (3.8).

< Предыдущая		Следующая >