3.1. Линейные дифференциальные уравнения высших порядков

Дифференциальное уравнение -го порядка называется Линейным, если неизвестная функция и все ее производные входят в уравнение линейно, то есть если уравнение имеет вид

, (3.1)

Где , , , …, – некоторые функции независимой переменной, называемые коэффициентами дифференциального уравнения, а функция называется правой частью. Пусть все функции , , непрерывны в интервале и .

Разделим уравнение (3.1) почленно на коэффициент при старшей производной и обозначим

, , .

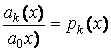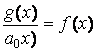Тогда уравнение (3.1) примет вид

. (3.2)

При этом все функции , , и непрерывны в .

Разрешим уравнение (3.2) относительно

.

Продифференцируем правую часть этого равенства по , , , …, . Производные будут соответственно равны:

, , …, .

Поскольку эти функции непрерывны в , то в силу теоремы Коши решение уравнения (3.2) с начальными условиями (1.2) существует и единственно.

Если правые части уравнений (3.1) и (3.2) равны нулю, то линейные уравнения называются Однородными. Однородное линейное уравнение имеет вид:

. (3.3)

Если же в уравнении (3.2) , то линейное уравнение называется Неоднородным. Вначале будут рассматриваться только однородные линейные уравнения, то есть уравнения вида (3.3).

< Предыдущая		Следующая >