2.4. Уравнения, приводящиеся к точным производным

Пусть левая часть дифференциального уравнения (2.1) является точной производной по независимой переменной некоторой функции . В этом случае порядок этого уравнения понижается на единицу. Действительно, уравнение (2.1) можно переписать в виде

.

Следовательно, если функция является решением дифференциального уравнения, то производная от функции тождественно равна нулю. Значит, сама функция равна постоянной величине и мы получим первый интеграл

.

Таким образом, задача свелась к интегрированию уравнения порядка , содержащего одну произвольную постоянную.

Пример 2.5. Найти общее решение уравнения

.

Решение. Левая часть этого уравнения является точной производной от функции . Имеем:

, , , .

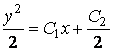Общее решение запишем в виде

.

Пример 2.6. Найти общее решение уравнения

.

Решение. В этом примере левая часть становится точной производной после деления уравнения на . Имеем:

, , , .

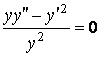
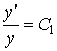Окончательно

.

< Предыдущая		Следующая >