2.3. Уравнение, однородное относительно искомой функции с ее производными

Пусть дифференциальное уравнение (2.1) имеет вид

, (2.5)

Где – однородная функция относительно , , . Для такой функции при любом допустимом справедливо тождество

. (2.6)

В этом случае положим , где – новая неизвестная функция. Тогда , и отсюда для второй производной получим:

, ,

То есть

.

Подставляя выражения для и в исходное дифференциальное уравнение (2.6), получим

.

В силу свойства однородности (2.6) имеем

.

Сокращая это равенство на , получим

,

То есть придём к дифференциальному уравнению первого порядка

.

Пусть – его общее решение. Это значит, что

.

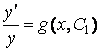Интегрируя это равенство, имеем

.

Поэтому общее решение исходного дифференциального уравнения (2.6)

.

Пример 2.4. Найти общее решение уравнения

.

Решение. Это уравнение однородно относительно , , , поскольку для него выполняется свойство (2.6) при . Поэтому полагаем:

, .

Подставляя эти выражения в исходное дифференциальное уравнение, получим

.

Сокращая это уравнение на , имеем

,

То есть

.

Это уравнение Бернулли. Разделим его на и получим

.

Обозначая , придем к линейному уравнению

.

Запишем для него однородное уравнение

.

Решая это уравнение, получим:

, , .

Решение линейного уравнения ищем в виде

.

Подстановка в это уравнение дает:

, , .

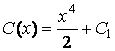Следовательно,

, .

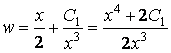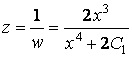Для исходной функции имеем дифференциальное уравнение первого порядка с разделяющимися переменными

.

Интегрируя это уравнение, получим

,

Откуда

.

Окончательно запишем общее решение в виде

.

< Предыдущая		Следующая >