2.2. Уравнение, не содержащее независимую переменную

Пусть дифференциальное уравнение -го порядка (2.1) не содержит переменную , то есть имеет вид

. (2.4)

Порядок этого уравнения можно понизить на единицу подстановкой , где – новая неизвестная функция, а принимается за независимую переменную. В этом случае все производные , , надо выразить через производные от функции по :

, ,

, … .

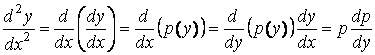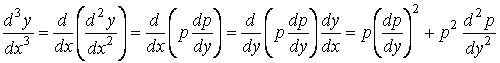Таким образом, любая производная выражается через производные от по порядка не выше , что и приводит к понижению порядка уравнения (2.4) на единицу.

Пример 2.3. Найти общее решение уравнения

.

Решение. Полагая , определим

.

Тогда получим уравнение первого порядка

,

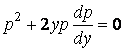То есть при

.

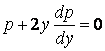Отсюда

, , , .

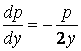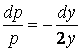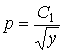Поскольку , то

, , .

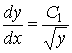Окончательно получим общее решение

.

Пусть теперь . Тогда , а это значит, что . Однако, это решение содержится в полученном общем решении исходного уравнения при . Следовательно, при сокращении на потери решения не происходит.

< Предыдущая		Следующая >