1.2. Общее и частное решения уравнения высшего порядка

Полученная функция (1.6) является решением дифференциального уравнения (1.4), поскольку при ее подстановке в это уравнение мы получили тождество . Более того, функция (1.6) определяет множество всех возможных решений уравнения (1.4), поэтому (1.6) является общим решением этого уравнения. Таким образом, общее решение дифференциального уравнения второго порядка содержит две произвольные постоянные и , то есть является двухпараметрическим.

Для определения частного решения по данному общему решению уже недостаточно одной точки , соответствующей начальному условию, а необходимо также задавать угловой коэффициент наклона интегральной кривой в этой точке, то есть необходимо задавать два начальных условия:

, .

Общее решение дифференциального уравнения -го порядка (1.1) или (1.2) имеет вид

, (1.7)

Где , , …, – произвольные постоянные. Их число всегда равно порядку дифференциального уравнения.

Произвольные постоянные , , …, должны быть независимыми. Например, выражение содержит две произвольные постоянные, но они не независимы, так как

.

Так что выражение фактически содержит одну постоянную.

Аналогично выражение

Фактически содержит две произвольные постоянные, так как .

В выражении же произвольные постоянные и независимы.

Возьмем общее решение уравнения (1.2), которое дается формулой (1.7), и придадим произвольным постоянным , , …, некоторые конкретные значения , , …, . Получим конкретное решение

. (1.8)

Это решение уравнения (1.2) называется Частным решением.

Для нахождения конкретного частного решения из общего решения задают начальные условия:

, , , …, . (1.9)

Число начальных условий всегда равно порядку дифференциального уравнения.

Дадим в заключение полное формальное определение общего решения дифференциального уравнения -го порядка.

Функция (1.7) называется Общим решением дифференциального уравнения (1.2), если:

1) при любых конкретных , , …, функция (1.8) удовлетворяет этому уравнению;

2) для любых допустимых начальных условий (1.9) возможно однозначно определить значения произвольных постоянных , , …, .

Пример 1.1. Доказать, что функция

Является общим решением дифференциального уравнения

.

Доказательство. Проверим выполнение двух условий общего решения.

1. Докажем, что функция является решением уравнения при любых и . Имеем:

, .

Подставляя вторую производную в уравнение , получим тождество .

2. Покажем, что для любых начальных условий

,

Значения произвольных постоянных и возможно определить однозначно. Подставляя начальные условия в выражения для и имеем систему уравнений:

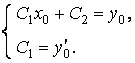
Решая эту систему, получим:

, .

То есть при любых значениях , и произвольные постоянные и определяются однозначно.

Тем самым доказано, что функция является общим решением дифференциального уравнения .

< Предыдущая		Следующая >