1.3. Теорема Коши для дифференциальных уравнений высших порядков

Условия существования и единственности частного решения дифференциального уравнения (1.2) при начальных условиях (1.8) даётся теоремой Коши.

Теорема Коши. Если правая часть дифференциального уравнения -го порядка вида (1.2) непрерывна как функция аргументов в некоторой окрестности точки , то найдется интервал независимой переменной , на котором существует решение уравнения (1.2), удовлетворяющее начальным условиям (1.8). Если при этом функция имеет ограниченные частные производные

, , …,

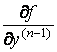
В области , то такое решение единственно.

Для случая область , используемая в теореме Коши, принадлежит трёхмерному пространству.

Задача, состоящая в решении уравнения (1.2) при начальных условиях (1.8) называется Задачей Коши для дифференциального уравнения -го порядка.

< Предыдущая		Следующая >