4.2. Уравнение Лагранжа

Уравнением Лагранжа называется дифференциальное уравнение вида

, (4.4)

Линейное относительно и . Здесь и – известные функции, причем . Введем параметр и получим

. (4.5)

Продифференцируем это равенство по переменной , полагая что

,

То есть

. (4.6)

Отсюда

.

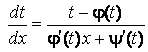Полагая, что , перепишем это дифференциальное уравнение в виде

,

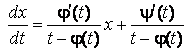То есть

.

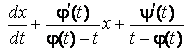Это линейное уравнение для функции . Интегрируя его, получим

.

Подставляя это в (4.5), получим вместе с последним равенством общее решение уравнения Лагранжа (4.4) в параметрической форме:

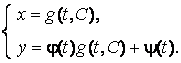
При определении этого общего решения мы полагали, что . Пусть теперь – корень уравнения . Таких корней может быть и несколько. В этом случае и уравнение (4.6) имеет решение . Подставляя это в (4.5), получим

,

То есть

.

Эта функция также является решением исходного уравнения. Это решение, вообще говоря, особое, однако в ряде случаев оно может быть и общим.

Пример 4.4. Решить уравнение

.

Решение. Полагаем . Тогда

.

Дифференцируя это равенство по переменной , имеем

.

Если , то

.

В данном случае нет надобности приводить уравнение к виду , так как при сразу возможно разделение

.

Отсюда

,

То есть

.

Следовательно,

, , .

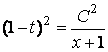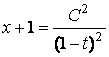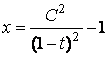Поэтому

.

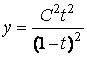Итак, параметрическая форма общего решения

В данном случае параметр можно исключить. Имеем:

, , .

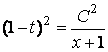Следовательно,

, ,

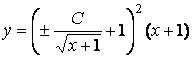То есть

.

Это и есть общее решение дифференциального уравнения.

Обратимся теперь к случаям, когда и . Эти числа для данного примера являются корнями уравнения . Корню отвечает решение , а для корня получим . Первое решение является особым, а второе – частным, так как оно появляется из общего решения при .

< Предыдущая		Следующая >