4.1. Простейшие уравнения, не разрешенные относительно производной

До сих пор предполагалось, что дифференциальное уравнение первого порядка

(4.1)

Разрешимо относительно , то есть приводимо к виду (1.5). Однако это возможно далеко не всегда. Для дифференциальных уравнений, не разрешенных относительно производных, можно сформулировать и доказать теорему о существовании и единственности решения при соответствующем начальном условии, а также рассмотреть основные методы интегрирования. Мы ограничимся рассмотрением простейших типов таких уравнений.

1. Уравнение не содержит аргумента и функции.

В этом случае дифференциальное уравнение (4.1) не содержит ни , ни , то есть имеет вид

. (4.2)

Это алгебраическое уравнение относительно производной . Пусть существует по крайней мере один действительный корень данного уравнения, где – постоянная величина. Интегрируя уравнение , получим:

, .

Но является корнем уравнения (4.2). Следовательно, общий интеграл этого уравнения

.

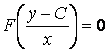Пример 4.1. Уравнение

Имеет вещественный корень . Поэтому общий интеграл этого уравнения

.

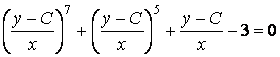2. Уравнение не содержит аргумента.

Пусть дифференциальное уравнение (4.1) не содержит аргумента и разрешимо относительно функции , то есть имеет вид

.

В этом случае вводится обозначение параметра . Тогда для получим параметрическое уравнение

, (4.3)

Откуда . Поскольку , то

, .

Интегрируя последнее равенство, имеем

.

Вычисляя этот неопределённый интеграл, представим переменную в параметрическом виде

,

Где – произвольная постоянная. Объединяя это равенство с равенством (4.3), получим общее решение дифференциальное уравнения в параметрическом виде:

В некоторых случаях параметр можно исключить из этой системы.

Пример 4.2. Решить уравнение

.

Решение. Полагаем . Тогда

, .

Имеем

.

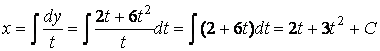Итак, общее решение

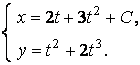
3. Уравнение не содержит функции.

Дифференциальное уравнение (4.1) не содержит функции и разрешимо относительно аргумента , то есть имеет вид

.

Введем параметр и получим параметрическое представление переменной

,

Откуда . Поскольку , то

, .

Интегрируя последнее равенство, имеем

.

Вычисляя неопределённый интеграл, получим

,

Где – произвольная постоянная. Итак, получено общее решение дифференциальное уравнения в параметрическом виде:

Параметр в ряде случаев можно исключить из этой системы.

Пример 4.3. Решить уравнение

.

Решение. Полагаем . Тогда

.

Имеем:

,

.

Получено общее решение

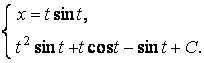
< Предыдущая		Следующая >