3.5. Нахождение ортогональных траекторий семейств кривых
Пусть имеются два семейства линий. Линии одного семейства называются Ортогональными траекториями линий другого семейства, если они пересекают линии второго семейства под прямым углом.
Пусть имеется уравнение семейства линий
.
Составим систему уравнений:
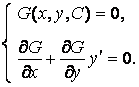
Исключая произвольную постоянную 
из этой системы, найдем дифференциальное уравнение исходного семейства
. (3.7)
Угловые коэффициенты касательных к кривым заданного семейства 
и к искомым ортогональным траекториям 
должны удовлетворять в каждой точке 
условию ортогональности
.
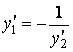Поскольку производная 
, 
и 
для исходного семейства удовлетворяют соотношению (3.7), то , и для семейства ортогональных траекторий должны удовлетворять дифференциальному уравнению
.
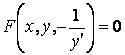Его общий интеграл
,
Очевидно, и будет алгебраическим уравнением семейства ортогональных траекторий.
Пример 3.9. Найти ортогональные траектории семейства парабол
.
Решение. Дифференцируя это равенство по переменной , имеем
.
Отсюда
.
Подставляя это выражение для произвольной постоянной в исходное уравнение, получим
,
То есть
.
Это дифференциальное уравнение исходного семейства. Заменяя в нем на 
, найдем дифференциальное уравнение семейства ортогональных траекторий
.
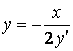То есть
, 
, 
.
Интегрируя последнее равенство, получим уравнение ортогональных траекторий
.
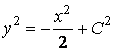Представляя это уравнение в виде
,
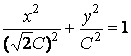Заключаем, что это семейство подобных эллипсов с полуосями 
и .
| < Предыдущая | Следующая > |
|---|
