3.4. Составление дифференциального уравнения по его общему решению

Пусть известен общий интеграл некоторого дифференциального уравнения первого порядка

. (3.5)

Покажем, как найти это уравнение. Для этого продифференцируем равенство (1.14) по переменной

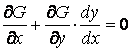. (3.6)

Составить дифференциальное уравнение первого порядка – значит найти соотношение между , и . Но для этого достаточно исключить произвольную постоянную из системы уравнений (3.5) и (3.6):

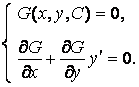
В результате получим новое уравнение, связывающее , и вида

.

Это и есть искомое дифференциальное уравнение. С геометрической точки зрения его называют дифференциальным уравнением семейства кривых (3.5).

Пример 3.8. Найти дифференциальное уравнение семейства окружностей

.

Решение. Имеем систему уравнений

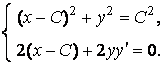
Отсюда

, .

Итак, искомое уравнение

,

То есть

.

Окончательно

.

< Предыдущая		Следующая >