3.3. Особые решения уравнения первого порядка

Точка называется Особой точкой дифференциального уравнения первого порядка (3.1), если в ней нарушается либо существование, либо единственность решения этого уравнения. Геометрически это означает, что через особую точку или не проходит ни одна интегральная кривая, или же проходит несколько интегральных кривых.

Наличие особых точек дифференциального уравнения (3.1) обусловлено нарушением для него условий теоремы Коши. Чаще всего это происходит из-за отсутствия непрерывности функций или . Именно это и приводит либо к отсутствию решения дифференциального уравнения, либо к нарушению его единственности.

Рассмотрим примеры особых точек.

Пример 3.5. Решим уравнение с разделяющимися переменными:

, , , , .

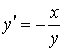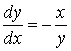Поскольку ни одна из окружностей не проходит через точку (0, 0), то эта точка особая.

Пример 3.6. Решим уравнение:

, , , , .

Этой задаче удовлетворяет бесчисленное множество парабол, проходящих через точку (0, 0), поэтому эта точка особая.

Функция называется Особым решением уравнения первого порядка (3.1), если она тождественно удовлетворяет этому уравнению и при этом её график полностью состоит из особых точек этого уравнения.

Поскольку через каждую точку кривой заведомо проходит одна интегральная кривая, а именно сама , то особые решения для всех точек кривой означают, что через каждую из них проходит еще, по крайней мере, одна интегральная кривая.

Пример 3.7. Решим уравнение с разделяющимися переменными

, , .

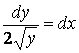Итак, общее решение представляет семейство полупарабол

. (3.3)

Кроме этого решения данное уравнение имеет и решение , а, значит, ось также является интегральной кривой. Но все точки оси особые, так как через каждую из них проходят две интегральные кривые ось и одна из полупарабол. Поэтому решение особое. В то же время его нельзя получить из (3.3) ни при каком значении . Это значит, что решение не может быть получено из общего решения, а, значит, оно не является частным. Именно в этом и состоит «особенность» этого решения.

Таким образом, в отличие от частных решений дифференциального уравнения, которые могут быть получены по его общему решению на основании заданного начального условия, особые решения невозможно получить из общего решения ни при каком значении произвольной постоянной .

Предположим, что для уравнения (3.1) функции и всюду непрерывны. Тогда для этого уравнения в любой точке выполняются условия теоремы Коши, то есть в любой точке имеют место и наличие, и единственность решения. Иными словами, такое уравнение особых точек не имеет, а, значит, оно не имеет и особых решений. Поэтому для таких уравнений можно говорить, что общее решение – это совокупность всех решений этого уравнения. Примером такого уравнения может служить

.

Особые решения уравнения (3.1) следует искать там, где либо функция , либо терпят разрывы на множестве точек. Например, для уравнения будет

,

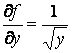И при и любом функция разрывная. Именно в связи с этим функция оказалась особым решением этого уравнения.

Существует и другой признак наличия особого решения. Пусть – общее решение уравнения (3.1). Предположим, что соответствующее семейство кривых имеет огибающую . Тогда функция является решением уравнения (3.1). Действительно, для любой точки на огибающей для соответствующей функции и для функции величины , , будут одни и те же, а, значит, и соотношения между ними будут одинаковыми для обеих функций.

Таким образом, функция является решением уравнения (3.1). Но через каждую точку огибающей проходят две интегральные кривые: сама линия и одна из линий . Следовательно, огибающая семейства кривых является графиком особого решения этого уравнения.

Уравнение огибающей семейства кривых находится путем исключения параметра из системы уравнений

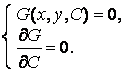. (3.4)

Если общий интеграл дифференциального уравнения представляет семейство кривых вида , то в случае существования огибающей этого семейства ее уравнение можно найти из системы (3.4). Это и будет особое решение данного дифференциального уравнения.

< Предыдущая		Следующая >