3.6. Метод последовательных приближений
Условия существования и единственности решения задачи Коши приводятся в теореме Коши, но даже при выполнении этих условий большинство дифференциальных уравнений не допускают нахождения точного решения. В этом случае применяются приближенные методы интегрирования. Выведем формулу одного из таких методов – метода последовательных приближений.
Рассмотрим задачу Коши, которая заключается в решении дифференциального уравнения (3.1) с заданным начальным условием (3.2):
![]() ,
, ![]() . (3.7)
. (3.7)
Предположим, что ![]() – решение задачи Коши (3.7). Тогда
– решение задачи Коши (3.7). Тогда
![]() .
.
Интегрируя это тождество, получим
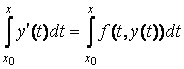 .
.
Отсюда следует, что
 .
.
Учитывая начальное условие задачи Коши (3.7), получим для нее интегральное уравнение
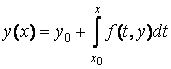 . (3.8)
. (3.8)
Итак, если ![]() есть решение задачи Коши (3.7), то оно удовлетворяет и интегральному уравнению (3.8).
есть решение задачи Коши (3.7), то оно удовлетворяет и интегральному уравнению (3.8).
Обратно, если функция ![]() есть решение интегрального уравнения (3.8), то, во-первых,
есть решение интегрального уравнения (3.8), то, во-первых, ![]() , а во-вторых, по теореме Барроу
, а во-вторых, по теореме Барроу ![]() . Следовательно, всякое решение интегрального уравнения (3.8) является и решением задачи Коши (3.7).
. Следовательно, всякое решение интегрального уравнения (3.8) является и решением задачи Коши (3.7).
Таким образом, интегральное уравнение (3.8) эквивалентно задаче Коши (3.7). Поэтому мы можем использовать интегральное уравнение (3.8) для решения задачи Коши.
В уравнении (3.8) справа под знаком интеграла находится неизвестная функция ![]() . Положим в качестве начального приближения решения
. Положим в качестве начального приближения решения ![]() и определим функцию
и определим функцию
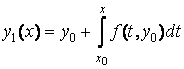 .
.
Положим в правой части интегрального уравнения (3.8) ![]() и определим
и определим
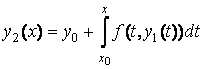 .
.
Итак, приближения решения задачи Коши находятся по рекуррентной формуле
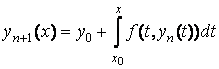 ,
, ![]() (3.9)
(3.9)
Теорема Пикара. Если в задаче Коши функция ![]() непрерывна и удовлетворяет условию Липшица по переменной
непрерывна и удовлетворяет условию Липшица по переменной ![]() , то существует единственное решение задачи Коши, к которому равномерно сходятся при
, то существует единственное решение задачи Коши, к которому равномерно сходятся при ![]() приближения, определяемые формулой (3.9).
приближения, определяемые формулой (3.9).
Теорема Пикара утверждает, что при выполнении условий этой теоремы последовательность функций ![]() ,
, ![]() ,
, ![]() , …, найденных по формуле (3.9), равномерно сходится к решению задачи Коши
, …, найденных по формуле (3.9), равномерно сходится к решению задачи Коши ![]() , то есть
, то есть
![]() .
.
Действительно, выполняя в формуле (3.9) предельный переход при ![]() , получим интегральное уравнение
, получим интегральное уравнение
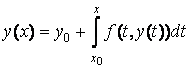 .
.
Это интегральное уравнение совпадает с уравнением (3.8), поэтому ![]() есть решение задачи Коши.
есть решение задачи Коши.
Метод последовательных приближений, основанный на формуле (3.9), также называется методом Пикара.
Пример 3.10. Решить задачу Коши
![]() ,
, ![]() .
.
Решение. Сводим задачу к интегральному уравнению
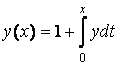 .
.
Задавая ![]() , последовательно находим:
, последовательно находим:
 ,
,
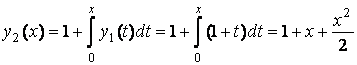 ,
,
. . . . . . . . . . . . . . . . . . . . .
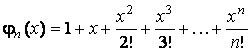 .
.
При ![]() получим справа степенной ряд для функции
получим справа степенной ряд для функции ![]() . Следовательно,
. Следовательно,
![]() .
.
Поэтому ![]() . Это же решение исходной задачи Коши можно получить как решение уравнения с разделяющимися переменными.
. Это же решение исходной задачи Коши можно получить как решение уравнения с разделяющимися переменными.
| < Предыдущая | Следующая > |
|---|