2.7. Интегрирующий множитель
Предположим, что для уравнения (2.16) условие (2.17) не выполняется. Тогда оно не является уравнением в полных дифференциалах. Возникает вопрос, можно ли умножить обе части уравнения (2.16) на такую функцию 
, что новое уравнение
Уже будет уравнением в полных дифференциалах. Если такая функция существует, то она называется Интегрирующим множителем.
Предположим, что – интегрирующий множитель. Тогда
,
Откуда
. (2.18)
Для нахождения получено уравнение в частных производных, которое интегрируется значительно сложнее, чем исходное уравнение. Поэтому найти интегрирующий множитель в общем случае удаётся очень редко. Задача намного упрощается, если этот множитель зависит только от одной переменной 
или 
.
Пусть сначала 
. Тогда из равенства (2.18)
.
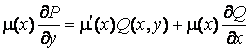Отсюда
, 
.
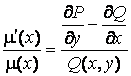Поскольку левая часть последнего уравнения зависит только от , то и правая часть не содержит . Положим для краткости
.
Получим:
, 
.
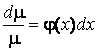Отсюда
.
Итак, одним из интегрирующих множителей является функция
. (2.19)
Проведенные рассуждения верны только в том случае, если интегрирующий множитель, зависящий только от , существует. Покажем, как об этом можно узнать заранее. Составим выражение
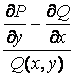
И предположим, что оно зависит только от . Обозначим его через 
и вычислим 
по формуле (2.19). Докажем, что это для исходного уравнения есть интегрирующий множитель.
Возьмем уравнение
. (2.20)
Имеем:
,
.
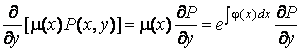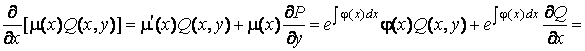
Итак, если вычислено по формуле (2.19), то уравнение (2.20) является уравнением в полных дифференциалах, а значит – интегрирующий множитель. Таким образом, зависимость выражения
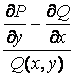
Только от есть необходимое и достаточное условие того, что уравнение (2.16) имеет интегрирующий множитель .
Аналогично уравнение (2.16) имеет интегрирующий множитель тогда и только тогда, когда
,
То есть когда левая часть не содержит . В этом случае
.
Пример 2.6. Решить дифференциальное уравнение
.
Решение. Имеем:
.
А значит, интегрирующий множитель существует и равен
.
Умножая исходное уравнение на 
, получим
.
Это уравнение в полных дифференциалах и оно интегрируется обычным образом.
| < Предыдущая | Следующая > |
|---|
