2.6. Уравнения в полных дифференциалах

Дифференциальное уравнение

(2.16)

Называется Уравнением в полных дифференциалах, если левая часть уравнения представляет собой полный дифференциал некоторой функции двух независимых переменных, то есть

.

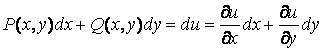Отсюда следует, что

, , , .

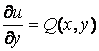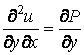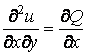По теореме Шварца смешанные частные производные второго порядка дважды дифференцируемой функции тождественно равны

.

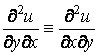Таким образом, для того, чтобы дифференциальное уравнение (2.16) было уравнением в полных дифференциалах, для входящих в него функций должно выполняться условие

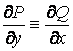. (2.17)

В этом случае уравнение (2.16) приводится к виду и будет общим интегралом этого уравнения. Решение уравнения (2.16) сводится к нахождению функции двух переменных по её полному дифференциалу. Это можно сделать способом, известным из математического анализа, с использованием криволинейного интеграла второго рода. Условие (2.17) означает, что такой интеграл не зависит от дуги интегрирования, а зависит только от начальной и конечной точек

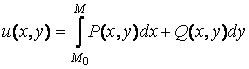
Однако существует и второй способ, который представим на конкретном примере.

Пример 2.5. Решить дифференциальное уравнение

.

Решение. Для этого уравнения

, .

Тогда

,

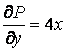Таким образом, условие (2.17) выполняется, а значит, мы имеем уравнение в полных дифференциалах. Остается найти такую функцию , что

.

Имеем

.

Интегрируя это равенство, получим

,

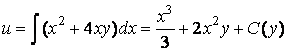Где – произвольная функция. Подберем так, чтобы было

.

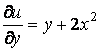Получим

.

Следовательно

, .

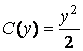Значит

.

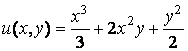Итак, общий интеграл исходного уравнения

.

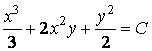< Предыдущая		Следующая >