2.5. Уравнение Риккати

Дифференциальное уравнение

, (2.13)

Где , , – известные функции, называется Уравнением Риккати.

Если , , – постоянные, то уравнение Риккати интегрируется разделением переменных

.

В случае уравнение (2.13) оказывается линейным, а при – уравнением Бернулли. В общем случае уравнение Риккати не интегрируется в квадратурах. Рассмотрим некоторые свойства этого уравнения.

Теорема. Если известно одно частное решение уравнения Риккати, то его общее решение может быть получено с помощью квадратур.

Доказательство. Пусть известно частное решение уравнения (50), тогда

. (2.14)

Полагая , где – новая искомая функция, по уравнению (2.13) в силу равенства (2.14) получим уравнение Бернулли

.

Поскольку уравнение Бернулли интегрируется в квадратурах, теорема доказана.

Пример 2.4. Проинтегрировать уравнение Риккати

,

Если известно его частное решение .

Решение. Полагая , для функции получим , откуда

.

Решением исходного уравнения будет функция

.

Частным случаем уравнения (2.13) является Специальное уравнение Риккати

, (2.15)

Где , , – постоянные.

При имеем

И уравнение интегрируется разделением переменных.

При получим

.

Полагая , где – новая неизвестная функция, найдем

, .

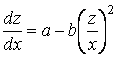Это однородное уравнение и оно интегрируется в квадратурах.

Кроме и существует еще бесконечное множество других значений , при которых специальное уравнение Риккати (2.15) интегрируется в квадратурах. Они задаются формулой

, .

При всех остальных значениях решение уравнения (2.15) не выражается в квадратурах и при задании начального условия может быть получено одним из численных методов.

< Предыдущая		Следующая >