2.4. Уравнение Бернулли

Уравнением Бернулли называется дифференциальное уравнение

, (2.11)

В котором левая часть линейна, а в правой части – некоторое число, , . Если , то получим линейное уравнение, если же , придем к уравнению с разделяющимися переменными. Разделим обе части уравнения (2.11) на

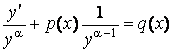. (2.12)

Положим 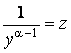, где – новая неизвестная функция. Тогда

, , .

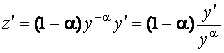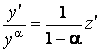Поэтому уравнение (2.12) перепишем в виде

.

Итак, уравнение Бернулли всегда может быть сведено к линейному дифференциальному уравнению. Решая его относительно , определим решение уравнения Бернулли

.

Пример 2.3. Решить дифференциальное уравнение

.

Решение. Разделим уравнение на

.

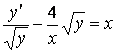Полагая , откуда 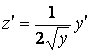, получим линейное уравнение

.

Решаем соответствующее однородное уравнение:

, , , , .

Поэтому решение неоднородного линейного уравнения ищем в виде

.

Поскольку , то подстановка в линейное уравнение дает

,

Откуда

, , .

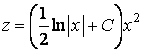Переходя к исходной функции , окончательно получим

.

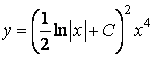< Предыдущая		Следующая >