2.2. Уравнения, приводящиеся к однородным

К однородным дифференциальным уравнениям приводятся некоторые уравнения первого порядка. Рассмотрим дифференциальное уравнение

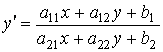. (2.3)

В общем случае это уравнение не является однородным.

Если , то имеем однородное уравнение

.

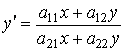Для общего случая уравнения (2.3) положим , где и – новые аргумент и неизвестная функция, и – неизвестные пока числа. Уравнение (2.3) примет теперь вид.

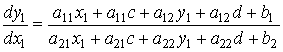. (2.4)

Потребуем, чтобы выполнялась система равенств

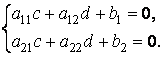
Предположим, что

.

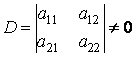Тогда система имеет единственное решение, то есть и находятся из нее единственным способом. При таких и уравнение (2.4) принимает вид

,

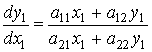То есть является однородным дифференциальным уравнением.

Предположим теперь, что , то есть что

.

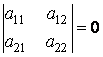Но в этом случае , то есть . Тогда уравнение (2.3) примет вид

.

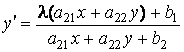Обозначим , откуда

.

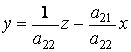Поэтому уравнение принимает вид

,

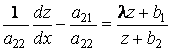А это уравнение с разделяющимися переменными.

Проведенные рассуждения верны и для уравнений вида

,

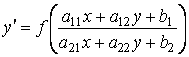Где – произвольная непрерывная функция.

< Предыдущая		Следующая >